如图，在平面直角坐标系中，O是坐标原点，一次函数与x轴正半轴交于点A，与y轴负半轴交于点B，OB=1，tan∠OBA=3，点C是射线AO上的一个动点（点C不与点O，A重合）．把线段CO绕点C顺时针旋转90°，得到的对应线段为CO1，点D是CO1的中点，连接AD，设点C坐标为（n,0），△ACD的面积为S．
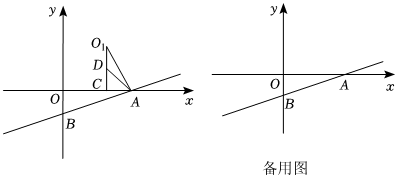
（1）求点A坐标；
（2）求当点C为OA中点时S的值；
（3）请求出S与n的函数表达式；
（4）当以A、C、D为顶点的三角形与△AOB相似时，请直接写出满足条件的n的值．
【考点】一次函数综合题．
【答案】（1）点A坐标为（3，0）；
（2）；
（3）
；
（4）或或-6．
（2）
S
=
9
16
（3）
S
=
- 1 4 n 2 + 3 4 n （ 0 ＜ n ＜ 3 ） |
1 4 n 2 - 3 4 n （ n ＜ 0 ） |
（4）
n
=
18
7
6
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/22 1:0:8组卷：49引用：2难度：0.5
相似题
-
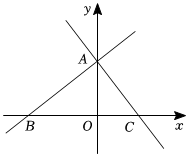1．如图，在平面直角坐标系中，直线y=kx+b与x轴交于点B（-5，0），与y轴交于点A，直线过点A，与x轴交于点C，点P是x轴上方一个动点．y=-43x+4
（1）求直线AB的函数表达式；
（2）若点P在线段AB上，且S△APC=S△AOB，求点P的坐标；
（3）当 S△PBC=S△ABC时，动点M从点B出发，先运动到点P，再从点P运动到点C后停止运动．点M的运动速度始终为每秒1个单位长度，运动的总时间为t（秒），请直接写出t的最小值．发布：2025/5/22 18:30:2组卷：670引用：1难度：0.3 -
2．给出如下定义：对于线段PQ，以点P为中心，把点Q逆时针旋转60°得到点R，点R叫做线段PQ关于点P的“完美点”．
例如等边△ABC中，点C就是线段AB关于点A的“完美点”．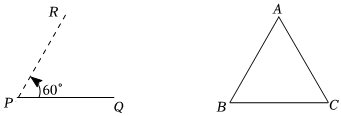
在平面直角坐标系xOy中．
（1）已知点A（0，2），在A1（，1），A2（-3，1），A3（1，3），A4（1，-3）中，是线段OA关于点O的“完美点”；3
（2）直线y=x+4上存在线段BB′，若点B′恰好是线段BO关于点B的“完美点”，求线段BB′的长；
（3）若OC=4，OE=2，点D是线段OC关于点O的“完美点”，点F是线段EO关于点E的“完美点”．当线段DF分别取得最大值和最小值时，直接写出线段CE的长．发布：2025/5/22 15:30:1组卷：595引用：1难度：0.1 -
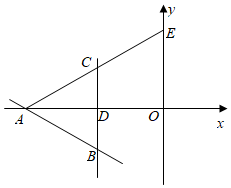3．如图，直线y=-x-6与x轴交于点A，点B（-6，m）也在该直线上，点B关于x轴的对称点为点C，直线BC交x轴于点D，点E坐标为（0，12）．112
（1）m的值为 ，点C的坐标为 ；
（2）求直线AC的函数表达式；
（3）晶晶有个想法：“设S=S△ABD+S四边形DCEO.由点B与点C关于x轴对称易得S△ABD=S△ACD，而△ACD与四边形DCEO拼接后可看成△AOE，这样求S便转化为直接求△AOE的面积．”但经反复演算，发现S△AOE≠S，请通过计算解释她的想法错在哪里？发布：2025/5/23 2:30:1组卷：268引用：4难度：0.5
