 阅读与思考,同学们通过“真阅读工程”活动接触到很多课外阅读,其中有一段文章与勾股定理的内容相关:在直角坐标系中,已知两点的坐标是M(x1,y1),N(x2,y2),求M、N两点之间的距离,可以通过MN2=|x2-x1|2+|y2-y1|2变形为MN=(x2-x1)2+(y2-y1)2计算.
阅读与思考,同学们通过“真阅读工程”活动接触到很多课外阅读,其中有一段文章与勾股定理的内容相关:在直角坐标系中,已知两点的坐标是M(x1,y1),N(x2,y2),求M、N两点之间的距离,可以通过MN2=|x2-x1|2+|y2-y1|2变形为MN=(x2-x1)2+(y2-y1)2计算.
试根据以上知识解决下列问题:
(1)若点M1(4,5),N1(7,10),则M1,N1两点间的距离为 3434;
(2)若点M2(-2,m)与N2(6,-1)的距离为10,求m的值;
(3)若点M3(2,2),N3(5,-5),点O是坐标原点,试判断△M3ON3是什么三角形,并说明理由.
M
N
2
=
|
x
2
-
x
1
|
2
+
|
y
2
-
y
1
|
2
(
x
2
-
x
1
)
2
+
(
y
2
-
y
1
)
2
34
34
【答案】
34
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/22 8:0:10组卷:104引用:1难度:0.5
相似题
-
 1.如图,在△ABC中,AB=AC,AD平分∠BAC,E为AC中点,若AD=4,BC=6,则DE的值为( )发布:2025/5/23 6:30:1组卷:76引用:1难度:0.5
1.如图,在△ABC中,AB=AC,AD平分∠BAC,E为AC中点,若AD=4,BC=6,则DE的值为( )发布:2025/5/23 6:30:1组卷:76引用:1难度:0.5 -
 2.如图,在△ABC中,BC=2,∠C=45°,BE⊥AC于点E,点D为CE的中点,连接BD,若BD=AB,则AB的长为( )2发布:2025/5/23 7:30:1组卷:12引用:1难度:0.5
2.如图,在△ABC中,BC=2,∠C=45°,BE⊥AC于点E,点D为CE的中点,连接BD,若BD=AB,则AB的长为( )2发布:2025/5/23 7:30:1组卷:12引用:1难度:0.5 -
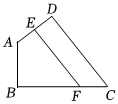 3.如图,四边形ABCD,AB=AD=10,CB=CD=20,∠B=∠D=90°,E是AD的中点,过点E作EF∥DC交BC于F,则EF的长为 .发布:2025/5/23 8:0:2组卷:49引用:3难度:0.4
3.如图,四边形ABCD,AB=AD=10,CB=CD=20,∠B=∠D=90°,E是AD的中点,过点E作EF∥DC交BC于F,则EF的长为 .发布:2025/5/23 8:0:2组卷:49引用:3难度:0.4


