如图，直线MN与直线PQ相交于O，∠POM=40°，点A在射线OP上运动，点B在射线OM上运动，AC、BC分别是∠BAO和∠ABO的角平分线．
（1）若∠BAO=50°，试求出∠ACB的度数；
（2）点A、B在运动的过程中，∠ACB的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出∠ACB的度数；
（3）在（2）的条件下，在△ABC中，如果有一个角是另一个角的4倍，请直接写出∠BAC的度数．
【考点】三角形内角和定理．
【答案】（1）110°；
（2）∠ACB的大小不变，理由见解答；
（3）∠BAC=27.5°或42.5°或14°或56°．
（2）∠ACB的大小不变，理由见解答；
（3）∠BAC=27.5°或42.5°或14°或56°．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/23 19:0:2组卷：285引用：2难度：0.4
相似题
-
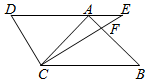1．将一副三角板如图放置，使点A落在DE上，AB与CE交于点F，若BC∥DE，则∠BFE的度数为（ ）发布：2025/6/17 23:30:2组卷：1087引用：3难度：0.8 -
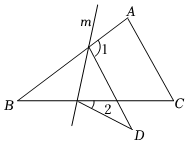2．如图，在△ABC中，将△ABC沿直线m翻折，点B落在点D的位置，若∠1-∠2=60°，则∠B的度数是（ ）发布：2025/6/17 23:30:2组卷：2907引用：15难度：0.6 -
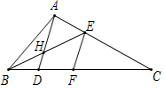3．如图，在△ABC中，点D在BC上，∠ADB=∠BAC，BE平分∠ABC，过点E作EF∥AD，交BC于点F．
（1）求证：∠BAD=∠C；
（2）若∠C=20°，∠BAC=110°，求∠BEF的度数．发布：2025/6/17 23:30:2组卷：1594引用：6难度：0.5
