在综合与实践课上，老师组织同学们以“矩形的折叠”为主题开展数学活动．
如图，在矩形ABCD中，AB=6，BC=10．
（1）如图①，将矩形ABCD折叠，使顶点B落在边AD上的点E处，折痕的一端点G在边BC上．当折痕的另一端点F在边AB上，且AF=2时，∠BGE的度数为 60°60°；
（2）如图②，将矩形ABCD折叠，使顶点A落在边BC上的点G处，折痕的一端点E在边AD上，另一端点为矩形ABCD的顶点B．将△ABE折叠后重新展开，连接BE，EC，过点E作EF⊥EC交线段AB于点F，连接CF，与BE交于点P．求PE长；
（3）如图③，将△EDH沿直线EH折叠，连接EC，折叠后点D落在EC边上的点D′处，点H在边CD上，过点D′作D′N⊥AD于点N，与EH交于点M，且AE=2．求△MD′H的面积．
【考点】四边形综合题．
【答案】60°
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/2 8:0:9组卷：301引用：1难度：0.3
相似题
-
1．如图1，在直线l上找一点C，使AC+BC最短，并在图中标出点C．
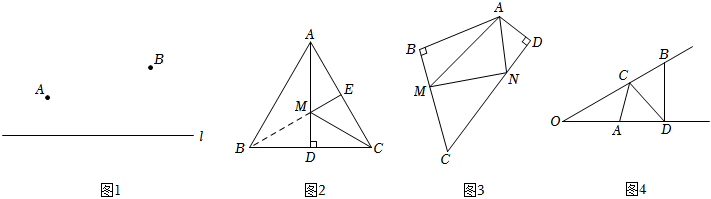
【简单应用】
（1）如图2，在等边△ABC中，AB=10，AD⊥BC，E是AC的中点，M是AD上的一点，求EM+MC
的最小值，借助上面的模型，由等边三角形的轴对称性可知，B与C关于直线AD对称，连接BM，
EM+MC的最小值就是线段 的长度，则EM+MC的最小值是 ；
（2）如图3，在四边形ABCD中，∠BAD=140°，∠B=∠D=90°，在BC，CD上分别找一点M、N，
当△AMN周长最小时，∠AMN+∠ANM=°．
【拓展应用】
如图4，是一个港湾，港湾两岸有A、B两个码头，∠AOB=30°，OA=1千米，OB=2千米，现有一艘货船从码头A出发，根据计划，货船应先停靠OB岸C处装货，再停靠OA岸D处装货，最后到达码头B．怎样安排两岸的装货地点，使货船行驶的水路最短？请画出最短路线并求出最短路程．发布：2025/6/14 2:0:1组卷：166引用：1难度：0.1 -
2．天府新区某校数学活动小组在一次活动中，对一个数学问题作如下探究：
（1）问题发现：如图1，在等边△ABC中，点P是边BC上任意一点，连接AP，以AP为边作等边△APQ，连接CQ．求证：BP=CQ；
（2）变式探究：如图2，在等腰△ABC中，AB=BC，点P是边BC上任意一点，以AP为腰作等腰△APQ，使AP=PQ，∠APQ=∠ABC，连接CQ．判断∠ABC和∠ACQ的数量关系，并说明理由；
（3）解决问题：如图3，在正方形ADBC中，点P是边BC上一点，以AP为边作正方形APEF，Q是正方形APEF的中心，连接CQ．若正方形APEF的边长为6，CQ=2，求正方形ADBC的边长．2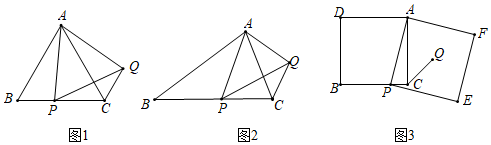
发布：2025/6/13 22:0:1组卷：2504引用：13难度：0.2 -
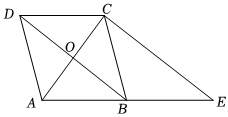3．如图，将平行四边形DBEC沿BD折叠，点C恰好落在EB的延长线上点A处，连接AC，BD交于点O，AC=6，BD=8．若直线AE上有一点F，当△FCE为等腰三角形时，线段AF的长为 ．发布：2025/6/14 1:30:1组卷：199引用：1难度：0.1
