如图，矩形ABCD中，AB=4，AD=3，点E在射线BC上，点F在CB的延长线上，且CF=CE，DF交直线AB于点G．
（1）求证：△BGF∽△CDE；
（2）若BG=1，求DE的长；
（3）当点E、F运动时，△DEG的面积是否改变？若不变，求出它的值；若改变，试用x（设BF=x）表示△DEG的面积．
【考点】相似形综合题．
【答案】（1）证明见解答过程；
（2）DE的长是4；
（3）当点E、F运动时，△DEG的面积保持不变，总等于12．
（2）DE的长是4
2
（3）当点E、F运动时，△DEG的面积保持不变，总等于12．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/17 11:0:4组卷：27引用：1难度：0.1
相似题
-
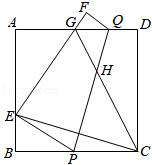1．如图，将正方形纸片ABCD沿PQ折叠，使点C的对称点E落在边AB上，点D的对称点为点F，EF交AD于点G，连接CG交PQ于点H，连接CE，EH．
（1）求证：△PBE∽△QFG；
（2）求∠ECG的度数；
（3）求证：EG2-CH2=GQ•GD．发布：2025/5/25 21:0:1组卷：400引用：2难度：0.3 -
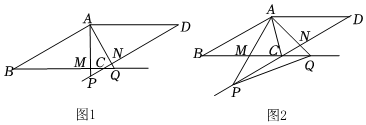2．如图1，在菱形ABCD中，∠ABC是锐角，P、Q分别是边DC、BC延长线上的动点，连接AP、AQ分别交BC、DC于点M、N．
（1）当AP⊥BC且∠PAQ=∠D时，证明：△ABM≌△ADN；
（2）如图2，当∠PAQ=∠BCD时，连接AC、PQ．12
①证明：AC2=CP•CQ；
②若AB=4，AC=2，则当CM为何值时，△APQ是以PQ为底边的等腰三角形．发布：2025/5/25 21:30:1组卷：184引用：1难度：0.1 -
3．如图，已知平行四边形ABCD中，
，AB=5，tanA=2，点E是射线AD上一动点，过点E作EF⊥AD，垂足为点E，交射线AB于点F，交射线CB于点G，联结CE、CF．设AE=m.AD=5
（1）如图，当点E在边AD上时．
①求证：△AEF∽△BGF．
②当S△DCE=4S△BFG时，求AE：ED的值．
（2）当点E在边AD的延长线上时，是否存在这样的点E使△AEF与△CFG相似？如果存在求出此时AE的长度．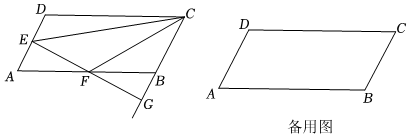
发布：2025/5/26 2:0:6组卷：86引用：1难度：0.2
