一数学兴趣小组为了测量校园内灯柱AB的高度,设计了以下三个方案:
方案一:在操场上点C处放一面平面镜,从点C处后退1m到点D处,恰好在平面镜中看到灯柱的顶部A点的像;再将平面镜向后移动4m(即FC=4m)放在F处.从点F处向后退1.5m到点H处,恰好再次在平面镜中看到灯柱的顶部A点的像,测得的眼睛距地面的高度ED、GH为1.5m、已知点B,C,D,F,H在同一水平线上,且GH⊥FH,ED⊥CD,AB⊥BH.(平面镜的大小忽略不计)
方案二:利用标杆CD测量灯柱的高度.已知标杆CD高1.5m,测得DE=2m,CE=2.5m.
方案三:利用三角板的边CE保持水平,并且边CE与点M在同一直线上.已知两条边CE=0.4m,EF=0.2m,测得边CE离地面距离DC=1.5m.
三种方案中,方案 二、三二、三不可行,请选择可行的方案求出灯柱的高度.

【答案】二、三
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/8/1 8:0:9组卷:95引用:1难度:0.5
相似题
-
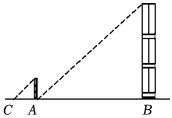 1.小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为 .发布:2025/6/18 9:0:1组卷:793引用:9难度:0.7
1.小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为 .发布:2025/6/18 9:0:1组卷:793引用:9难度:0.7 -
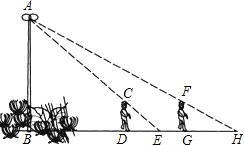 2.如图,花丛中有一路灯杆AB.在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米.如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).发布:2025/6/18 8:0:2组卷:1489引用:49难度:0.1
2.如图,花丛中有一路灯杆AB.在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米.如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).发布:2025/6/18 8:0:2组卷:1489引用:49难度:0.1 -
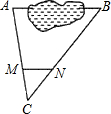 3.如图,A,B两点被池塘隔开,在AB外任选一点C,连接AC,BC,在AC,BC上分别取其靠近C点的三等分点M,N.量得MN=38m,则AB的长为m.发布:2025/6/18 11:0:1组卷:128引用:1难度:0.5
3.如图,A,B两点被池塘隔开,在AB外任选一点C,连接AC,BC,在AC,BC上分别取其靠近C点的三等分点M,N.量得MN=38m,则AB的长为m.发布:2025/6/18 11:0:1组卷:128引用:1难度:0.5


