直线y1=ax+b和抛物线y2=ax2+bx（a,b是常数，且a≠0）在同一平面直角坐标系中，直线y1=ax+b经过点（-4，0）．下列结论：①抛物线y2=ax2+bx的对称轴是直线x=-2；②抛物线y2=ax2+bx与x轴一定有两个交点；③关于x的方程ax2+bx=ax+b有两个根x1=-4，x2=1；④若a＞0，当x＜-4或x＞1时，y1＞y2.其中正确的结论是（ ）
y
2
=
a
x
2
+
bx
y
2
=
a
x
2
+
bx
y
2
=
a
x
2
+
bx
【答案】B
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/9 1:0:8组卷：983引用：6难度：0.5
相似题
-
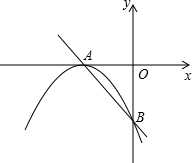1．如图，直线y=-x-2交x轴于点A，交y轴于点B，抛物线y=ax2+bx+c的顶点为A，且经过点B．
（1）求该抛物线的解析式；
（2）若点C（m,-）在抛物线上，求m的值．92
（3）根据图象直接写出一次函数值大于二次函数值时x的取值范围．发布：2025/6/14 0:0:1组卷：742引用：4难度：0.3 -
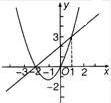2．二次函数y=ax2+bx+c和一次函数y=mx+n的图象如图所示，则ax2+bx+c≤mx+n时，x的取值范围是 ．发布：2025/6/14 2:0:1组卷：869引用：42难度：0.5 -
3．已知二次函数y=ax2+c的图象与一次函数y=mx+n的图象相交于A（-2，p），B（1，q）两点，则关于x的不等式ax2-mx+c＞n的解集是 ．
发布：2025/6/13 23:0:1组卷：732引用：2难度：0.5
相关试卷
