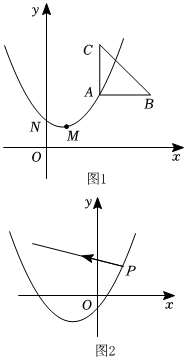
如图1，在Rt△ABC中，∠BAC=90°，A（2，2），AC∥y轴．AC=AB=2，抛物线L：y=-t+12（x+t）2的顶点为M、与y轴交于点N
（1）写出M的坐标；（用含t的代数式表示）
（2）求点N最低时t的值；
（3）在L的位置随t的值变化而变化的过程中，说明抛物线的顶点M与点C能否重合，并求点M在△ABC内部所经过路线的长：
（4）如图2，当t=1时，抛物线L：y=-1+12（x+1）2将此时L在-2023≤x≤2023这个范围的曲线段，记为W某同学设计了一个动画，以P（1，1）为端点的射线所在直线的解析式为y=mx+n光点从点P出发，沿射线飞行．若击中W上（点P除外）的整点（横、纵坐标均为整数），且m也为整数时，抛物线L就发光、直接写出此时整数m的个数．
y
=
-
t
+
1
2
（
x
+
t
）
2
L
：
y
=
-
1
+
1
2
（
x
+
1
）
2
【考点】二次函数综合题．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/9 3:0:9组卷：281引用：1难度：0.2
相似题
-
1．定义：与坐标轴不重合的直线交坐标轴于A、B两点（A、B不重合），若抛物线L过点A，点B，则称此抛物线为直线的“友谊线”
（1）若抛物线L为直线y=-x+3的“友谊线”，且过点（-1，0），求此抛物线的解析式；
（2）已知直线y=kx+b的“友谊线”为y=-x2+12x+1，且直线与双曲线y=12交于M，N，求线段MN的长；2x
（3）若有直线y=mx+n,且m+n=1，对任意的非零实数a,一定存在其“友谊线”为抛物线L：y=ax2+bx+c,求b的取值范围．发布：2025/6/22 1:0:1组卷：587引用：5难度：0.4 -
2．在平面直角坐标系xOy中，抛物线y=ax2+
x+c与y轴交于点C，与x轴交于A、B两点（点A在点B的左侧），其中A（-233，0），tan∠ACO=3．33
（1）求抛物线的解析式；
（2）如图1，点D为直线BC上方抛物线上一点，连接AD、BC交于点E，连接BD，记△BDE的面积为S1，△ABE的面积为S2，求的最大值；S1S2
（3）如图2，将抛物线沿射线CB方向平移，点C平移至C′处，且OC′=OC，动点M在平移后抛物线的对称轴上，当△C′BM为以C′B为腰的等腰三角形时，请直接写出点M的坐标．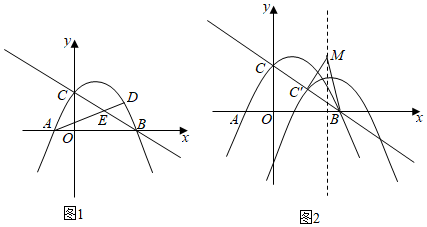
发布：2025/6/22 1:0:1组卷：1858引用：4难度：0.1 -
3．如图1，在平面直角坐标系中，抛物线y=ax2+bx+c经过A（3，0），D（-1，0），E（0，3），顶点为B．
（1）求抛物线的解析式；
（2）假设点S是直线AE上方抛物线上一动点，过点S作SG⊥AE，求当SG取得最大值时，点S的坐标；
（3）连接AB、AE、BE，设△AOE沿x轴正方向平移t个单位长度（0＜t≤3）时，△AOE与△ABE重叠部分的面积为S，求S与t之间的函数关系式，并指出t的取值范围．
发布：2025/6/22 1:0:1组卷：83引用：1难度：0.2
