从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 BB;(请选择正确的一个)
A.(a-b)2=a2-2ab+b2 B.(a+b)(a-b)=a2-b2 C.a(a+b)=a2+ab
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2-4y2=12,x+2y=4.求x-2y的值;
②若a32=128,求(a-1)(a+1)(a2+1)(a4+1)(a8+1)(a16+1)的值.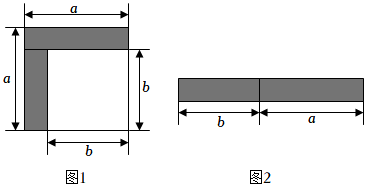
【考点】整式的混合运算—化简求值;平方差公式的几何背景.
【答案】B
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/5/27 8:0:10组卷:53引用:1难度:0.5
相似题
-
1.先化简再求值:(2a+b)(2a-b)-(a+2b)2+5b2,其中a=1,b=-1.
发布:2025/6/7 17:0:1组卷:85引用:2难度:0.6 -
2.小马虎在做一道化简求值题“(x+2)2+(2x+1)(2x-1)-4x(x+1),其中x=-2”时,把“x=-2”错看成了“x=2”,可他的计算结果跟同学一样,请你说明这是怎么回事?
发布:2025/6/7 17:30:1组卷:37引用:1难度:0.7 -
3.先化简,再求值:(x+y)(x-y)+y(x+2y)-(x-y)2,其中x=2+
,y=2-5.5发布:2025/6/7 17:30:1组卷:30引用:4难度:0.8


