问题情境：
我们知道，“两条平行线被第三条直线所截，同位角相等，内错角相等，同旁内角互补”，所以在某些探究性问题中通过“构造平行线”可以起到转化的作用．
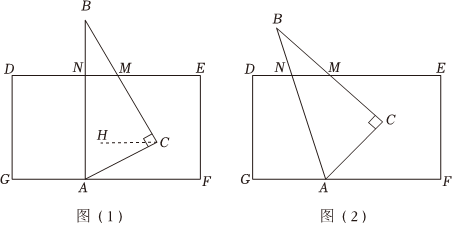
已知三角板ABC中，∠BAC=60°，∠B=30°，∠C=90°，长方形DEFG中，DE∥GF．
问题初探：
（1）如图（1），若将三角板ABC的顶点A放在长方形的边GF上，BC与DE相交于点M，AB⊥DE于点N，求∠EMC的度数；
分析：过点C作CH∥GF，则有CH∥DE，从而得∠CAF=∠HCA，∠EMC=∠MCH，从而可以求得∠EMC的度数；
由分析得，请你直接写出：∠CAF的度数为 30°30°，∠EMC的度数为 60°60°；
类比再探：
（2）若将三角板ABC按图（2）所示方式摆放（AB与DE不垂直），请你猜想写出∠CAF与∠EMC的数量关系，并说明理由．
【考点】平行线的判定与性质．
【答案】30°；60°
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/30 8:0:9组卷：73引用：1难度：0.5
相似题
-
1．阅读下面材料：
小颖遇到这样一个问题：已知：如图甲，AB∥CD，E为AB，CD之间一点，连接BE，DE，∠B=35°，∠D=37°，求∠BED的度数．
她是这样做的：
过点E作EF∥AB，
则有∠BEF=∠B．
因为AB∥CD，
所以EF∥CD．①
所以∠FED=∠D．
所以∠BEF+∠FED=∠B+∠D．
即∠BED=．
Ⅰ．小颖求得∠BED的度数为；
Ⅱ．上述思路中的①的理由是；
Ⅲ．请你参考她的思考问题的方法，解决问题：如图乙．
已知：直线a∥b,点A，B在直线a上，点C，D在直线b上，连接AD，BC，BE平分∠ABC，DE平分∠ADC，且BE，DE所在的直线交于点E．
（1）如图1，当点B在点A的左侧时，若∠ABC=α，∠ADC=β，则∠BED的度数为（用含有α，β的式子表示）．
（2）如图2，当点B在点A的右侧时，设∠ABC=α，∠ADC=β，直接写出∠BED的度数（用含有α，β的式子表示）．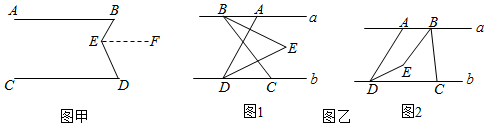
发布：2025/6/8 17:0:2组卷：317引用：2难度：0.6 -
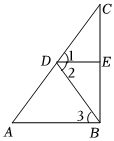2．如图，∠1=∠2，DE⊥BC，AB⊥BC，那么∠A=∠3吗？说明理由．
解：∠A=∠3，理由如下：
∵DE⊥BC，AB⊥BC（已知），
∴∠DEB=90°，∠ABC=（ ）．
∴∠DEB+=180°．
∴DE∥AB （ ）．
∴∠1=∠A （ ）．
∠2=∠3 （ ）．
∵∠1=∠2（已知），
∴∠A=∠3 （ ）．发布：2025/6/8 17:0:2组卷：43引用：1难度：0.5 -
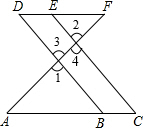3．填空完成推理过程：如图，E点为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D．试说明：AC∥DF．
解：∵∠1=∠2（已知）
∠1=∠3 （ ）；
∴∠2=∠3（等量代换）；
∴∥（ ）；
∴∠C=∠ABD （ ）；
又∵∠C=∠D（已知）；
∴∠D=∠ABD（等量代换）
∴AC∥DF （ ）．发布：2025/6/8 17:0:2组卷：94引用：7难度：0.7
