数学实践活动课上，研究小组探究如下问题：
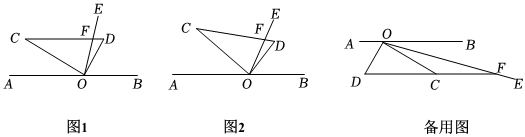
【问题情境】如图，点A，O，B在同一条直线上，将一直角三角尺如图1放置，使直角顶点与点O重合，其中∠COD=90°，∠C=30°，OE平分∠BOC且交CD所在直线于点F．
【独立思考】（1）若∠AOC=30°，求∠OFC的度数；
【实践操作】（2）如图2，将直角三角尺绕点O旋转，当∠OFC=2∠AOC时，求∠AOC的度数；
【深入探究】（3）继续旋转直角三角尺，若OC不与AB重合，试探究旋转过程中，∠AOC和∠OFC之间的数量关系．
【考点】三角形综合题．
【答案】（1）75°；
（2）40°；
（3）∠AOC=2∠OFC-120°或∠AOC=2∠OFC+120°．
（2）40°；
（3）∠AOC=2∠OFC-120°或∠AOC=2∠OFC+120°．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/5 8:0:9组卷：120引用：3难度：0.5
相似题
-
1．在平面直角坐标系xOy中，已知点A的坐标为（0，-1），点C（m,0）是x轴上的一个动点．
（1）如图1，点B在第四象限，△AOB和△BCD都是等边三角形，点D在BC的上方，当点C在x轴上运动到如图所示的位置时，连接AD，请证明△ABD≌△OBC；
（2）如图2，点B在x轴的正半轴上，△ABO和△ACD都是等腰直角三角形，点D在AC的上方，∠D=90°，当点C在x轴上运动（m＞1）时，设点D的坐标为（x,y），请探求y与x之间的函数表达式．
发布：2025/9/13 22:0:1组卷：99引用：1难度：0.3 -
2．已知△ABC中，AB=AC，点D为BC上一点，∠BAC=∠DAE，AD=AE，连接CE．
（1）当∠BAC=90°时，如图1，直接写出线段CE、CD、BC的数量关系；
（2）当∠BAC=120°时，如图2，求证：CE+CD=BC；
（3）在（2）的条件下，点G为AC的中点，连接BG，∠BAD=∠ABG，若AE=7，求BG的长．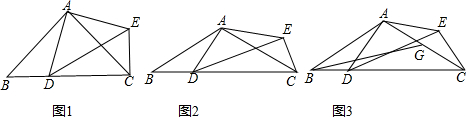
发布：2025/9/14 3:0:1组卷：95引用：1难度：0.3 -
3．将两块全等含有30°的直角三角板如图①摆放．
（1）将图①中的△A1B1C顺时针旋转45°得图②，点P1是A1C与AB的交点，点Q是A1B1与BC的交点，求证：CP1=CQ；
（2）在图②中，若AP1=2，则CQ等于多少？
（3）如图③，在B1C上取一点E，连接BE、P1E，设BC=1，当BE⊥P1B时，则△P1BE面积的最大值是．发布：2025/9/14 2:0:1组卷：50引用：1难度：0.3
