在△ABC中，若|cosA-32|+（22-cosB）2=0，则△ABC的形状是（ ）
|
cos
A
-
3
2
|
+
（
2
2
-
cos
B
）
2
=
0
【答案】B
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/23 11:0:2组卷：39引用：2难度：0.5
相似题
-
1．A，B是平面内的两个定点，在平面内找一点C，使△ABC构成等腰直角三角形，这样的C点可找（ ）
发布：2025/6/19 2:30:2组卷：74引用：1难度：0.7 -
2．如图，在△ABC中，AC=BC，∠ACB=90°，AE平分∠BAC交BC于E，BD⊥AE于D，DM⊥AC交AC的延长线于M，连接CD，给出四个结论：
①∠ADC=45°；②BD=AE；③AC+CE=AB；④AB-BC=2MC；其中正确的结论有（ ）12发布：2025/6/19 22:0:1组卷：769引用：21难度：0.9 -
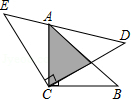3．如图，△ACB和△ECD都是等腰直角三角形，CA=CB=6，CE=CD，△ACB的顶点A在△ECD的斜边DE上，若AE：AD=1：2，则两个三角形重叠部分的面积为（ ）发布：2025/6/20 8:0:2组卷：1262引用：6难度：0.5
