类比一次函数和反比例函数的学习经验,某数学实验小组尝试探究“y=6|x|的函数图象与性质”,进行了如下活动.
(1)【小组合作讨论交流】
同学甲说:“我们可以从表达式分析,猜想图象位置.”
同学乙回应道:“是的,因为自变量x的取值范围是 x≠0x≠0,所以图象与y轴不相交.”
同学丙补充说:“又因为函数值y大于0,所以图象一定在第 一、二一、二象限.”
……
(2)【独立操作探究性质】
在平面直角坐标系中,画出y=6|x|的图象.
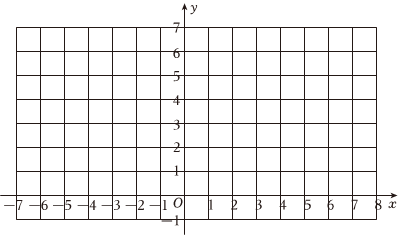
结合图象,描述函数图象与性质:
①函数y=6|x|的图象是两条曲线;
②该函数图象关于 y轴y轴对称:
③图象的增减性是 x>0时,y随x的增大而减小,x<0时,y随x的增大而增大;x>0时,y随x的增大而减小,x<0时,y随x的增大而增大;;
④同学丁说:“将第二象限的曲线绕原点顺时针旋转90°后,与第一象限的曲线重合.”请你判断同学丁的说法是否正确?若错误,举出反例:若正确,请说明理由.
(3)【拓展探究综合应用】
直接写出不等式的6|x|-x>5解集是 x<-3或-2<x<0或0<x<1x<-3或-2<x<0或0<x<1.
y
=
6
|
x
|
y
=
6
|
x
|
y
=
6
|
x
|
6
|
x
|
-
x
>
5
【考点】反比例函数与一次函数的交点问题.
【答案】x≠0;一、二;y轴;x>0时,y随x的增大而减小,x<0时,y随x的增大而增大;;x<-3或-2<x<0或0<x<1
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/30 8:0:9组卷:575引用:2难度:0.5
相似题
-
 1.如图,已知点A(a,3)是一次函数y1=x+b图象与反比例函数y2=图象的一个交点.6x
1.如图,已知点A(a,3)是一次函数y1=x+b图象与反比例函数y2=图象的一个交点.6x
(1)求一次函数的解析式;
(2)在y轴的右侧,当y1>y2时,直接写出x的取值范围.发布:2025/6/19 9:0:1组卷:1126引用:55难度:0.7 -
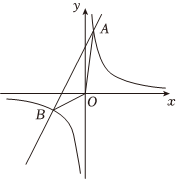 2.如图,已知反比例函数y=与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m).k1x
2.如图,已知反比例函数y=与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m).k1x
(1)求k1、k2、b的值;
(2)求△AOB的面积;
(3)若M(x1,y1)、N(x2,y2)是反比例函数y=图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并简要说明理由.k1x发布:2025/6/19 9:0:1组卷:3097引用:69难度:0.5 -
 3.如图,正比例函数y1=k1x和反比例函数y2=的图象交于A(1,2),B两点,给出下列结论:k2x
3.如图,正比例函数y1=k1x和反比例函数y2=的图象交于A(1,2),B两点,给出下列结论:k2x
①k1<k2;
②当x<-1时,y1<y2;
③当y1>y2时,x>1;
④当x<0时,y2随x的增大而减小.
其中正确的有( )发布:2025/6/19 8:30:1组卷:863引用:59难度:0.7


