旗下产品
充值服务
试卷征集
申请校本题库
智能组卷
错题库
五大核心功能
试卷征集
加入会员
操作视频

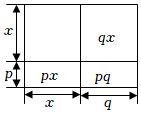
结合图，观察下列式子：
（x+p）（x+q）=x2+px+qx+pq
=x2+（p+q）x+pq
于是有：x2+（p+q）x+pq=（x+p）（x+q）．
（1）填空：因式分解x2+5x+6=（x+
2
2
）（x+
3
3
）；
（2）化简：
（
x
2
-
x
-
2
x
2
-
4
x
+
4
-
2
x
+
6
x
2
+
x
-
6
）
÷
x
x
-
2
；
（3）化简：
1
x
2
+
x
+
1
x
2
+
3
x
+
2
+
1
x
2
+
5
x
+
6
+
1
x
2
+
7
x
+
12
．

【考点】分式的混合运算；因式分解-十字相乘法等．
【答案】2；3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
当前模式为游客模式，立即登录查看试卷全部内容及下载
发布：2024/9/30 5:0:1组卷：518引用：3难度：0.5
相似题

  • 1．（1）计算：
    a
    2
    -
    b
    2
    a
    ÷（a-
    2
    ab
    -
    b
    2
    a
    ）；
    （2）解不等式组：
    3
    -
    4
    x
    ≥
    -
    5
    4
    3
    x
    +
    1
    ＜
    2
    x
    ．

    发布：2025/5/25 19:0:2组卷：243引用：2难度：0.7
    解析

  • 2．化简或计算：
    （1）
    （
    -
    1
    ）
    2021
    +
    8
    -
    4
    sin
    45
    °
    +
    |
    -
    2
    |
    +
    （
    1
    2
    ）
    -
    2
    ；
    （2）
    x
    2
    -
    9
    x
    2
    +
    2
    x
    +
    1
    ÷
    （
    x
    +
    3
    -
    x
    2
    x
    +
    1
    ）
    ．

    发布：2025/5/25 20:0:1组卷：154引用：4难度：0.6
    解析

  • 3．计算：
    （1）化简：
    a
    2
    -
    1
    a
    2
    -
    2
    a
    +
    1
    ÷
    a
    +
    1
    a
    -
    1
    +
    a
    a
    -
    1
    ；
    （2）解不等式组
    1
    2
    （
    x
    +
    1
    ）
    ≤
    2
    x
    +
    2
    2
    ＞
    x
    +
    3
    3
    ，并求出不等式组的整数解之和．

    发布：2025/5/25 20:30:1组卷：256引用：2难度：0.7
    解析
相关试卷
商务合作服务条款走进菁优
帮助中心兼职招聘意见反馈
深圳市菁优智慧教育股份有限公司
粤ICP备10006842号公网安备44030502001846号
©2010-2025 jyeoo.com 版权所有
深圳市市场监管
主体身份认证
APP开发者：深圳市菁优智慧教育股份有限公司| 应用名称：菁优网 | 应用版本：5.0.7 |隐私协议|第三方SDK|用户服务条款
广播电视节目制作经营许可证|出版物经营许可证|网站地图
本网部分资源来源于会员上传，除本网组织的资源外，版权归原作者所有，如有侵犯版权，请立刻和本网联系并提供证据，本网将在三个工作日内改正