疫情以来，越来越多的厂家转型为电商．某工厂在网上接到一批产品生产订单，按要求在15天内完成，约定这批产品的出厂价为每件20元，设第x天（1≤x≤15，x为整数）每件产品的成本是p元，p与x之间符合一次函数关系，部分数据如表：
| 天数（x） | 1 | 3 | 6 | 10 |
| 每件成本p（元） | 6.5 | 7.5 | 9 | 11 |
y
=
2 x + 20 （ 1 ≤ x ＜ 10 ， x 为整数 ） |
40 （ 10 ≤ x ≤ 15 ， x 为整数 ） |
（1）直接写出p与x,W与x之间的函数关系式，并注明自变量x的取值范围；
（2）求李师傅第几天创造的利润最大？最大利润是多少元？
（3）任务完成后，统计发现平均每个工人每天创造的利润为297元．工厂制定如下奖励制度：如果一个工人某天创造的利润超过该平均值，则该工人当天可获得20元奖金，请计算李师傅共可获得多少元奖金？
【答案】（1）p与x的函数关系式为：p=0.5x+6（1≤x≤15）；W与x之间的函数关系式为：W=
；
（2）第9天创造的利润最大，最大利润是361元；
（3）李师傅共可获得240元奖金．
- x 2 + 18 x + 280 | 1 ≤ x ＜ 10 |
- 20 x + 560 | 10 ≤ x ≤ 15 |
（2）第9天创造的利润最大，最大利润是361元；
（3）李师傅共可获得240元奖金．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/6 8:0:9组卷：66引用：1难度：0.5
相似题
-
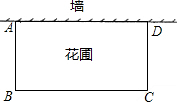1．张大爷要围成一个矩形花圃．花圃的一边利用足够长的墙另三边用总长为32米的篱笆恰好围成．围成的花圃是如图所示的矩形ABCD．设AB边的长为x米．矩形ABCD的面积为S平方米．
（1）求S与x之间的函数关系式（不要求写出自变量x的取值范围）；
（2）当x为何值时，S有最大值并求出最大值．
（参考公式：二次函数y=ax2+bx+c（a≠0），当x=-时，y最大（小）值=b2a）4ac-b24a发布：2025/6/24 19:0:1组卷：251引用：25难度：0.5 -
2．俄罗斯世界杯足球赛期间，某商店销售一批足球纪念册，每本进价40元，规定销售单价不低于44元，且获利不高于30%．试销售期间发现，当销售单价定为44元时，每天可售出300本，销售单价每上涨1元，每天销售量减少10本，现商店决定提价销售．设每天销售量为y本，销售单价为x元．
（1）请直接写出y与x之间的函数关系式和自变量x的取值范围；
（2）当每本足球纪念册销售单价是多少元时，商店每天获利2400元？
（3）将足球纪念册销售单价定为多少元时，商店每天销售纪念册获得的利润w元最大？最大利润是多少元？发布：2025/6/25 6:30:1组卷：6484引用：40难度：0.3 -
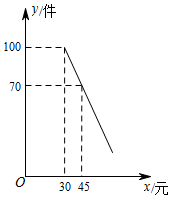3．为迎接国庆节，某商店购进了一批成本为每件30元的纪念商品，经调查发现，该商品每天的销售量y（件）与销售单价x（元）满足一次函数关系，其图象如图所示．
（1）求该商品每天的销售量y与销售单价x的函数关系式；
（2）若商店按不低于成本价，且不高于60元的单价销售，则销售单价定为多少元，才能使销售该商品每天获得的利润w（元）最大？最大利润是多少？发布：2025/6/25 8:30:1组卷：926引用：7难度：0.7
