在平面直角坐标系中，直线AC分别交x、y轴于点A、C，直线BC经过点C，交x轴于点B，OB=OC，tan∠OCA=23．AB=10．
（1）如图1，求点A的坐标；
（2）如图2，经过点B的直线交直线AC于点F，E为BC上一点，线段BF上一点D与点B、E的距离相等，设点E的横坐标为m,点D的横坐标为n,当tan∠ABF=3时，求n与m之间的函数关系式（不要求写出m的取值范围）；
（3）如图3，在（2）的条件下，连接AE，点M为x轴上点B右侧一点，连接DM，N为第一象限内一点，分别连接MN、DN，若AC=AE，∠NMD=2∠DMB，∠DNM-∠DMB=90°，MN=9105，求点M的坐标．
2
3
9
10
5
【考点】三角形综合题．
【答案】（1）A（-4，0）；
（2）；
（3）M（14，0）．
（2）
n
=
1
4
m
+
9
2
（3）M（14，0）．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/8 8:0:8组卷：15引用：2难度：0.1
相似题
-
1．（1）如图，△AOB和△COD是等腰直角三角形，∠AOB=∠COD=90°，点C在OA上，点D在线段BO延长线上，连接AD，BC．线段AD与BC的数量关系为 ．
（2）如图2，将图1中的△COD绕点O顺时针旋转α（0°＜α＜90°）第一问的结论是否仍然成立；如果成立，证明你的结论，若不成立，说明理由．
（3）如图3，若AB=8，点C是线段AB外一动点，，连接BC，若将CB绕点C逆时针旋转90°得到CD，连接AD，则AD的最大值是 ．AC=33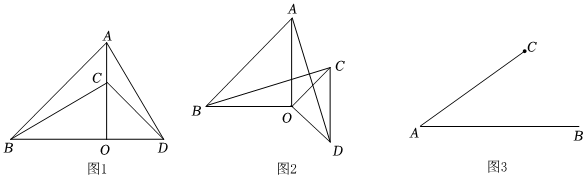
发布：2025/5/23 7:0:1组卷：274引用：4难度：0.3 -
2．（1）如图1，在△ABC中，点D为AC边上一点，AD=
CD，连接BD，过点A作AE∥BC交BD的延长线于点E，若S△ABC=24，则S△ABE=；12
（2）如图2，在△ABC中，AC=8，∠B=60°，求△ABC面积的最大值；
（3）公园作为城市生态环节的重要组成部分，从来都是衡量一座城市的生态底蕴和宜居指数的重要指标．西安高新区建区以来，始终坚持生态优先的绿色发展之路，高度重视公园、绿地建设，先后建成了新纪元公园、唐城墙遗址公园等一批综合性公园．近年来，进入发展“快车道”的西安高新区，更是把公园建设当做提升区域生态环境和城市品质的重要任务，近期高新区管委会拟在一片空地上修建一座矩形城市公园ABCD，如图3，按照规划，在这个矩形公园里要修建一个三角形活动中心△AEC，点E在AD边上，且DE：CD=1：，活动中心△AEC被景观大道EF（宽度不计）分割为△AEF和△ECF两块区域，已知EF=200米，且S△AEF=3；求当△AEC面积最大时矩形ABCD的面积．13S△AEC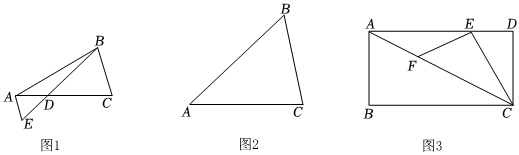
发布：2025/5/23 7:30:1组卷：487引用：1难度：0.1 -
3．在△ABC中，AB=AC，D为射线BC上一点，DB=DA，E为射线AD上一点，且AE=CD，连接BE．
（1）如图1，若∠ADB=120°，，求DE的长；AC=3
（2）如图2，若BE=2CD，连接CE并延长，交AB于点F，求证：CE=2EF；
（3）如图3，若BE⊥AD，垂足为点E，猜想AE、AD、BE的数量关系，并证明．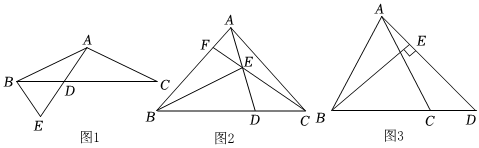
发布：2025/5/23 7:0:1组卷：203引用：1难度：0.1
