如图，在矩形ABCD中，∠DBC=30°，AB=4，点E是对角线BD上一动点，点E以1个单位长度/秒的速度从点D出发，向点B运动，运动时间为t.过点E作EM⊥AE，交BC于点M．
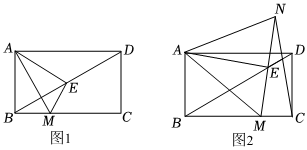
（1）如图1，当t=4时，求BM的长．
（2）点E在运动过程中，∠AME的大小是否发生变化？若变化，请说明理由；若不变，请求出∠AME的大小；
（3）如图2，点N是点M关于AE的对称点，连接CN，AN，求证：CN=MN．
【答案】（1）；
（2）不发生变化，为60°，理由见解答；
（3）见解答．
4
3
3
（2）不发生变化，为60°，理由见解答；
（3）见解答．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/13 8:0:8组卷：451引用：1难度：0.3
相似题
-
1．如图，在梯形ABCD中，AB∥CD，对角线AC、BD相交于点O，如果S△AOB=2S△AOD，AC=10，那么OC的长是．发布：2025/1/28 8:0:2组卷：107引用：1难度：0.4 -
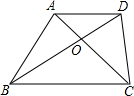2．如图，梯形ABCD中AD∥BC，对角线AC、BD交于0点，△AOD与△DOC的面积之比为3：7，则AD：BC=．发布：2025/1/28 8:0:2组卷：39引用：1难度：0.7 -
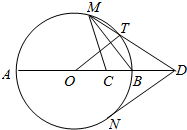3．如图，AB是圆O的直径，C是半径OB的中点，D是OB延长线上一点，且BD=OB，直线MD与圆O相交于点M、T（不与A、B重合），DN与圆O相切于点N，连接MC，MB，OT．
（Ⅰ）求证：DT•DM=DO•DC；
（Ⅱ）若∠DOT=60°，试求∠BMC的大小．发布：2025/1/28 8:0:2组卷：365引用：1难度：0.3
