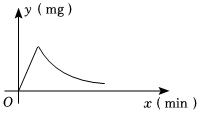
为预防传染病，某校定期对教室进行“药熏消毒”．已知某种药物在燃烧阶段，室内每立方米空气中的含药量y（mg）与燃烧时间x（min）成正比例；一次性燃烧完以后，y与x成反比例（如图所示）．在药物燃烧阶段，实验测得在燃烧5分钟后，此时教室内每立方米空气含药量为72mg.
（1）若一次性燃烧完药物需10分钟．
①分别求出药物燃烧时及一次性燃烧完以后y关于x的函数表达式．
②当每立方米空气中的含药量低于75mg时，对人体方能无毒害作用，那么从消毒开始，在哪个时间段学生不能停留在教室里？
（2）已知室内每立方米空气中的含药量不低于0.7mg时，才能有效消毒，如果有效消毒时间要持续120分钟，问要一次性燃烧完这种药物需多长时间？
7
2
7
5
【考点】反比例函数的应用．
【答案】（1）①y=x（0≤x≤10）；y=（x≥10）；
②当2≤x≤50时，学生不能在教室停留；
（2）要一次性燃烧完这种药物需11分钟．
7
10
70
x
②当2≤x≤50时，学生不能在教室停留；
（2）要一次性燃烧完这种药物需11分钟．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/11 8:0:9组卷：909引用：1难度：0.5
相似题
-
1．喝绿茶前需要烧水和泡茶两个工序，即需要将电热水壶中的水烧到100℃，然后停止烧水，等水温降低到适合的温度时再泡茶，烧水时水温y（℃）与时间x（min）成一次函数关系；停止加热过了1分钟后，水壶中水的温度y（℃）与时间x（min）近似于反比例函数关系（如图）．已知水壶中水的初始温度是20℃，降温过程中水温不低于20℃．
（1）分别求出图中所对应的函数关系式，并且写出自变量x的取值范围；
（2）从水壶中的水烧开（100℃）降到80℃就可以进行泡制绿茶，问从水烧开到泡茶需要等待多长时间？发布：2025/6/22 20:0:1组卷：1392引用：15难度：0.7 -
2．某物体质量一定，若体积V=40m3，则密度ρ=1.6kg/m3．
（1）写出此物体的密度ρ与体积V的函数关系式，并画出它的图象；
（2）当物体密度ρ=3.2kg/m3时，它的体积V是多少？
（3）若让该物体的体积控制在4m3～80m3之间，则该物体的密度是如何变化的？发布：2025/6/22 18:0:1组卷：40引用：4难度：0.7 -
3．心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化．开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数y随时间x（分钟）的变化规律如图所示（其中AB、BC分别为线段，CD为双曲线的一部分）：
（1）开始上课后第五分钟时与第三十分钟时相比较，何时学生的注意力更集中？
（2）一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？发布：2025/6/22 18:0:1组卷：3498引用：19难度：0.3
