问题发现：小星发现把几个图形拼成一个新的图形，再通过两种不同的方法计算同一个图形的面积，可以得到一个等式，也可以求出一些不规则图形的面积．
例如，由图1，可得到等式：（a+2b）（a+b）=a2+3ab+2b2．
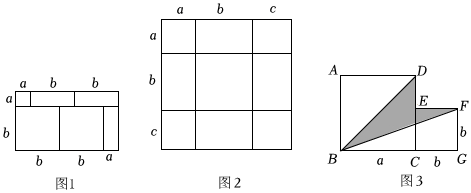
（1）类比探究：如图2，将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形，通过上面的启发，你能发现什么结论？请用等式表示出来．
（2）结论应用：已知a+b+c=14，ab+bc+ac=26，求a2+b2+c2的值．
（3）拓展延伸：如图，将两个边长分别为a和b的正方形拼在一起，B，C，G三点在同一直线上，连接BD和BF．若这两个正方形的边长满足a+b=8，ab=14，请求出阴影部分的面积．
【答案】（1）（a+b+c）2=a2+b2+c2+2ab+2bc+2ac；（2）144；（3）11．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/4 8:0:5组卷：103引用：1难度：0.5
相似题
-
1．已知a=2012x+2011，b=2012x+2012，c=2012x+2013，那么a2+b2+c2-ab-bc-ca的值等于（ ）
发布：2025/6/8 9:0:1组卷：605引用：3难度：0.8 -
2．已知x+y=6，xy=8，则x2y+xy2的值是 ．
发布：2025/6/8 8:0:6组卷：113引用：4难度：0.8 -
3．如图，现有边长为a的正方形1个，边长为b的正方形3个，边长为（a,b（a＞b）的长方形4个，把它们拼成一个大长方形，请利用这个拼图中图形的面积关系分解因式：a2+4ab+3b2=．
发布：2025/6/8 8:0:6组卷：145引用：5难度：0.8
