综合与实践：
问题情境：已知OM是∠AOB的平分线，P是射线OM上的一点，点C，D分别在射线OA，OB上，连接PC，PD．
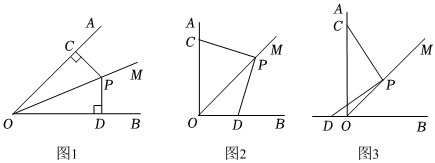
（1）初步探究：如图1，当PC⊥OA，PD⊥OB时，PC与PD的数量关系是 PC=PDPC=PD；
（2）深入探究：如图2，点C，D分别在射线OA，OB上运动，且∠AOB=90°，当∠CPD=90°时，PC与PD在（1）中的数量关系还成立吗？请说明理由；
（3）拓展应用：如图3，如果点C在射线OA上运动，且∠AOB=90°，当∠CPD=90°时，点D落在了射线OB的反向延长线上，若点P到OB的距离为3，OD=1，求OC的长（直接写出答案）．
【考点】全等三角形的判定与性质；角平分线的性质．
【答案】PC=PD
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/31 9:0:8组卷：176引用：4难度：0.5
相似题
-
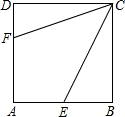1．如图，正方形ABCD的边长为6，点E、F分别在AB，AD上，若CE=3，且∠ECF=45°，则CF的长为（ ）5发布：2025/6/19 11:0:1组卷：5935引用：76难度：0.5 -
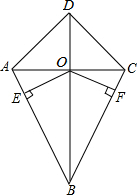2．我们把两组邻边相等的四边形叫做“筝形”．如图，四边形ABCD是一个筝形，其中AB=CB，AD=CD．对角线AC，BD相交于点O，OE⊥AB，OF⊥CB，垂足分别是E，F．求证OE=OF．发布：2025/6/19 11:0:1组卷：4362引用：85难度：0.7 -
3．如图，CA=CD，∠B=∠E，∠BCE=∠ACD．求证：AB=DE．发布：2025/6/19 11:0:1组卷：2175引用：67难度：0.7
