小云在学习过程中遇到一个函数y=16|x|（x2-x+1）（x≥-2）．下面是小云对其探究的过程，请补充完整：
（1）当-2≤x＜0时，对于函数y1=|x|，即y1=-x,当-2≤x＜0时，y1随x的增大而 减小减小，且y1＞0；对于函数y2=x2-x+1，-2≤x＜0当时，y2随x的增大而 减小减小，且y2＞0；结合上述分析，进一步探究发现，对于函数y,当-2≤x＜0时，y随x的增大而 减小减小．
（2）当x≥0时，对于函数y,当x≥0时，y与x的几组对应值如下表：
y
=
1
6
|
x
|
（
x
2
-
x
+
1
）
| x | 0 | 1 2 |
1 | 3 2 |
2 | 5 2 |
3 | ⋯ |
| y | 0 | 1 16 |
1 6 |
7 16 |
1 | 95 48 |
7 2 |
⋯ |
（3）过点（0，m）（m＞0）作平行于x轴的直线l,结合（1）（2）的分析，解决问题：若直线l与函数
y
=
1
6
|
x
|
（
x
2
-
x
+
1
）
（
x
≥
-
2
）
7
3
7
3
【考点】二次函数与不等式（组）．
【答案】减小；减小；减小；
7
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/20 3:0:1组卷：209引用：5难度：0.5
相似题
-
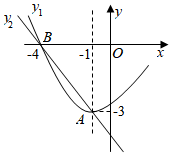1．如图是抛物线y1=ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标为A（-1，-3），与x轴的一个交点为B（-4，0）．点A和点B均在直线y2=kx+n（k≠0）上．下列结论错误的是（ ）发布：2025/5/25 12:30:1组卷：1216引用：4难度：0.1 -
2．阅读感悟：
“数形结合”是一种重要的数学思想方法，同一个问题有“数”、“形”两方面的特性，解决数学问题，有的从“数”入手简单，有的从“形”入手简单，因此，可能“数”→“形”或“形”→“数”，有的问题需要经过几次转化．这对于初、高中数学的解题都很有效，应用广泛．
解决问题：
已知，点M为二次函数y=-x2+2bx-b2+4b+1图象的顶点，直线y=mx+5分别交x轴正半轴和y轴于点A，B．
（1）判断顶点M是否在直线y=4x+1上，并说明理由；
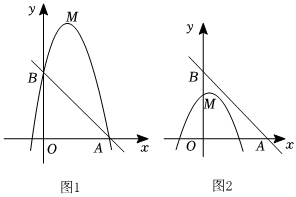
（2）如图1，若二次函数图象也经过点A，B，且mx+5＞-x2+2bx-b2+4b+1，结合图象，求x的取值范围；
（3）如图2，点A坐标为（5，0），点M在△AOB内，若点C（，y1），D（14，y2）都在二次函数图象上，试比较y1与y2的大小．34发布：2025/5/25 8:30:2组卷：195引用：2难度：0.4 -
3．已知抛物线y=ax2-4ax+3与x轴交于A，B两点（点A在点B的左侧），且AB=2．
（1）求该抛物线的解析式．
（2）关于x的不等式ax2-4ax+3＞0的解集为 ．
（3）点M（x1，y1），点N（x2，y2）是该抛物线上的两点，若x2-x1=2，试比较y1和y2的大小．发布：2025/5/25 20:0:1组卷：294引用：5难度：0.5
