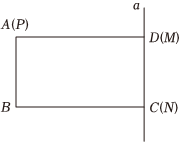
如图所示，长方形ABCD中，AB=4cm,AD=8cm.点P从点A出发，沿边AD向A-D-A做往返运动，每秒移动2cm,动直线a与边CD重合，交AD于点M，BC于点N．直线a与点P同时出发，沿DA方向移动，每秒移动1cm,移动t秒（t＞0），当直线a与边AB重合时，移动全部停止．
（1）用含t的代数式表示AP的长度；
（2）当t为何值时，点P在直线a上；
（3）连结PB，PN，直接写出当t为何值时，△PAB与△PMN全等．
【考点】全等三角形的判定．
【答案】（1）AP=
；（2）或8；（3）．
2 t （ 0 ＜ t ≤ 4 ） |
16 - 2 t （ 4 ＜ t ≤ 8 ） |
8
3
8
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/7 6:0:11组卷：492引用：3难度：0.5
