在正方形ABCD中，点P是对角线BD所在直线上的一点；点E在AD的延长线上，且PA=PE，连接CE．
（1）如图1，当点P在线段BD上时，线段PA与线段CE的数量关系是 CE=2PACE=2PA；
（2）如图2，当点P在BD的延长线上时，其它条件不变，则（1）中的结论是否仍然成立？若成立，请予以证明；若不成立，请说明理由；
（3）如图3，把正方形ABCD改为菱形ABCD，其它条件不变，当∠ABC=120°时，
①探究线段PA与线段CE的数量关系，并请直接写出你的结论；
②若AB=23，CE=6，请直接写出AE的长．
2
2
3
【考点】四边形综合题．
【答案】CE=PA
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/4 8:0:9组卷：446引用：3难度：0.3
相似题
-
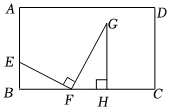1．如图，在矩形ABCD中，AB=6，BC=10，E是AB上一点，BE=2．F是BC上的动点，连接EF，H是CF上一点且=k（k为常数，k≠0），分别过点F，H作EF，BC的垂线，交点为G．设BF的长为x,GH的长为y.HFCF
（1）若x=4，y=6，则k的值是 ．
（2）若k=1时，求y的最大值．
（3）在点F从点B到点C的整个运动过程中，若线段AD上存在唯一的一点G，求此时k的值．发布：2025/5/24 9:30:2组卷：704引用：10难度：0.1 -
2．如图，两个全等的四边形ABCD和OA′B′C′，其中四边形OA′B′C′的顶点O位于四边形ABCD的对角线交点O．
回归课本
（1）如图1，若四边形ABCD和OA′B′C′都是正方形，则下列说法正确有 ．（填序号）
①OE=OF；②重叠部分的面积始终等于四边形ABCD的；③BE+BF=14DB．22
应用提升
（2）如图2，若四边形ABCD和OA′B′C′都是矩形，AD=a,DC=b,写出OE与OF之间的数量关系，并证明．
类比拓展
（3）如图3，若四边形ABCD和OA′B′C′都是菱形，∠DAB=α，判断（1）中的结论是否依然成立；如不成立，请写出你认为正确的结论（可用α表示），并选取你所写结论中的一个说明理由．
发布：2025/5/24 9:30:2组卷：269引用：2难度：0.1 -
3．综合与实践
数学活动：
数学活动课上，老师提出如下数学问题：
已知四边形ABCD与四边形BEFG都为正方形，P为DF的中点，连接AP，EP，如图1，当点E在AB上时，求证：AP=PE．
独立思考
（1）请你证明老师提出的问题；
合作交流
（2）解决完上述问题后，“翱翔”小组的同学受此启发，把正方形BEFG绕点B顺时针旋转，当点F落在对角线BD上时（如图2），他们认为老师提出的结论仍然成立．请你予以证明；
问题解决
（3）解决完上述问题后，“善思”小组提出如下问题，把正方形BEFG绕点B顺时针旋转（如图3），当点D，E，F在同一条直线上时，DE与BC交于点H．若AD=2，BG=2，请直接写出HC的值．2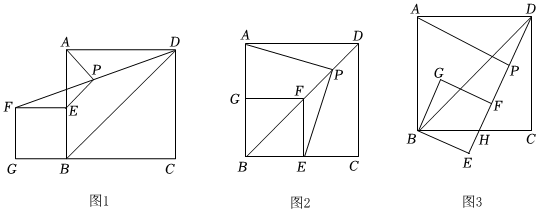
发布：2025/5/24 10:0:2组卷：621引用：1难度：0.4
