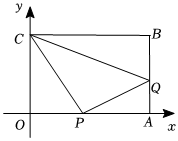
如图，在平面直角坐标系中，O是坐标原点，矩形OABC的两边分别在x轴和y轴上，点B的坐标为（12，8），现有两动点P，Q，点P以每秒3个单位的速度从点O出发向终点A运动，同时点Q以每秒2个单位的速度从点A出发向终点B运动，连接PC，PQ，CQ．设运动时间为t秒（t＞0）．
（1）点P的坐标为 （3t,0）（3t,0），点Q的坐标为 （12，2t）（12，2t）（用含t的代数式表示）；
（2）请判断四边形APCQ的面积是否会随时间t的变化而变化，并说明理由；
（3）若以A，P，Q为顶点的三角形与OCP相似时，请直接写出t的值．
【考点】相似形综合题．
【答案】（3t，0）；（12，2t）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/6 8:0:9组卷：292引用：5难度：0.2
相似题
-
1．如图，平行四边形ABCD中，CE⊥AB于E，CE=CD，AB=nAE，连接AC、DM⊥AC，垂足为M．
（1）求证：CM•EC=AE•DM；
（2）如图2，n=2，连接EM，求的值；EMMC
（3）如图3，连接BM，若BM=AB，直接写出sin∠EBM的值．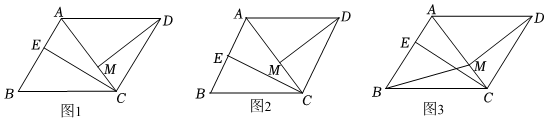
发布：2025/6/15 14:30:2组卷：48引用：1难度：0.1 -
2．在△ABC中，CD是中线，E，F分别为BC，AC上的一点，连接EF交CD于点P．
（1）如图1，若F为AC的中点，CE=2BE，求的值；DFEC
（2）如图2，设=m,CEBC=n（n＜CFAC），若m+n=4mn,求证：PD=PC；12
（3）如图3，F为AC的中点，连接AE交CD于点Q，若QD=QP，直接写出的值．BEEC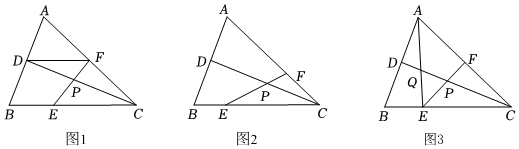
发布：2025/6/15 15:0:1组卷：334引用：2难度：0.3 -
3．矩形ABCD中，AB=nAD（n＞1），点P为对角线AC上的一个动点（不与A、C两点重合），过点P作直线MN⊥AC，分别交射线AB、射线AD于点M、N．
（1）如图1，当点N与点D重合时，求的值（用含有n的代数式表示）．PMPD
（2）如图2，当点M为AB边的中点，且DP=DA时，求n的值．
（3）如图3，当n=2，移动点P，使得△APD与△BPC相似，则的值=．AMAD
发布：2025/6/15 15:0:1组卷：107引用：1难度：0.2
