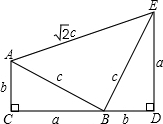
如图，四边形ACDE是证明勾股定理时用到的一个图形，a,b,c是Rt△ABC和Rt△BED边长，易知AE=2c，这时我们把关于x的形如ax2+2cx+b=0的一元二次方程称为“勾系一元二次方程”．
请解决下列问题：
（1）写出一个“勾系一元二次方程”；
（2）求证：关于x的“勾系一元二次方程”ax2+2cx+b=0必有实数根；
（3）若x=-1是“勾系一元二次方程”ax2+2cx+b=0的一个根，且四边形ACDE的周长是62，求△ABC面积．
AE
=
2
c
a
x
2
+
2
cx
+
b
=
0
a
x
2
+
2
cx
+
b
=
0
a
x
2
+
2
cx
+
b
=
0
2
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/2 1:0:1组卷：14746引用：39难度：0.1
相似题
-
1．如图，矩形ABCD中，AB=8cm,BC=6cm,点M从点A出发，沿着AB→BC的方向以4cm/s的速度向终点C匀速运动；点N从点B出发，沿着BC→CD的方向以3cm/s的速度向终点D匀速运动；点M，N同时出发，当M，N中任何一个点到达终点时，另一个点同时停止运动，点M运动时间为t（s），连接MN，△BMN的面积为S（cm2）．
（1）求S关于t的函数解析式，并直接写出自变量t的取值范围；
（2）△BMN的面积可以是矩形ABCD面积的吗？如能，求出相应的t值，若不能，请说明理由．14
发布：2025/1/13 8:0:2组卷：260引用：4难度：0.6 -
2．如图，在△ABC中，∠B=90°，点P从点A开始沿AB边向点B以1cm/秒的速度移动，点Q从点B开始沿BC边向点C以2cm/秒的速度移动．
（1）如果P、Q分别从A、B同时出发，几秒后△PBQ是等腰直角三角形？
（2）如果P、Q分别从A、B同时出发，几秒后△PBQ的面积等于3cm2？
（3）如果P、Q分别从A、B同时出发，四边形APQC的面积是△ABC面积的三分之二？发布：2025/1/20 8:0:1组卷：125引用：1难度：0.5 -
3．如图，在△ABC中，∠C=90°，AB=10cm,AC=8cm,点P，Q同时由A，C两点出发，分别沿AC，CB方向移动，它们的
速度都是2cm/s.
（1）设经过t秒后，那么在△PCQ中，此时线段，线段CQ长为cm,PC长为cm.
（2）经过几秒，P，Q相距cm？210发布：2025/1/24 8:0:2组卷：205引用：6难度：0.3
