【观察】如图1是小慧购买的某款黄金分制尺实物图，小慧观察测量发现：OA=OB，CB=CD，OE=EF=FC=CO．在阅读使用说明书后思考提出一些问题，请你完成下列的解答．
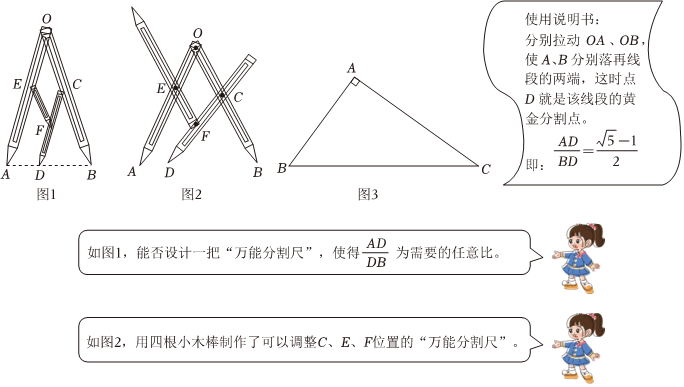
【思考】（1）在该黄金分制尺中OCCB应等于=5-125-12；
（2）根据小慧测量结果，求证：A、D、B三点共线；
【创新】（3）深度学习探究：根据上述对话，在OA=OB的条件下，至少再补充下列哪几个选项作为条件，才能制作出该尺．
①OE=CF；
②OC=CF；
③CD=CB；
④OE=OC；
⑤OC=EF，
我选择条件是 ①③⑤①③⑤；（填序号）
【应用】如图3，在△ABC中，∠BAC=90°，AB=1，AC=2，调节图2中C、E、F三点到适当位置，仅使用该分割尺，可直接作出以AC为直径的圆与边BC的交点D，请写出你的设计方案．（要求：写出点C，E、F必须满足的条件）
OC
CB
5
-
1
2
5
-
1
2
2
【考点】圆的综合题．
【答案】；①③⑤
5
-
1
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/12 8:0:8组卷：48引用：1难度：0.1
相似题
-
1．如图1，以点O为圆心，半径为4的圆交x轴于A，B两点，交y轴于C，D两点，点P为劣弧AC上的一动点，延长CP交x轴于点E；连接PB，交OC于点F．
（1）若点F为OC的中点，求PB的长；
（2）求CP•CE的值；
（3）如图2，过点O作OH∥AP交PD于点H，当点P在弧AC上运动时，连接AC，PC．试问△APC与△OHD相似吗？说明理由；的值是否保持不变？若不变，试证明，求出它的值；若发生变化，请说明理由．APDH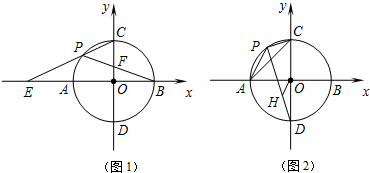
发布：2025/6/24 18:30:1组卷：272引用：1难度：0.5 -
2．下面是“用三角板画圆的切线”的画图过程．
如图1，已知圆上一点A，画过A点的圆的切线．画法：
（1）如图2，将三角板的直角顶点放在圆上任一点C（与点A不重合）处，使其一直角边经过点A，另一条直角边与圆交于B点，连接AB；
（2）如图3，将三角板的直角顶点与点A重合，使一条直角边经过点B，画出另一条直角边所在的直线AD．则直线AD就是过点A的圆的切线．
请回答：①这种画法是否正确 （是或否）；
②你判断的依据是：．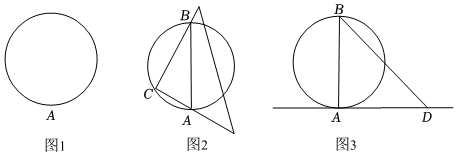
发布：2025/6/25 8:0:1组卷：19引用：1难度：0.4 -
3．如图，已知⊙O′与x轴交于A、B两点，与y轴交于C、D两点，圆心O′的坐标是（1，-1），半径为．5
（1）比较线段AB与CD的大小；
（2）求A、B、C、D四点的坐标；
（3）过点D作⊙O′的切线，试求这条切线的解析式．发布：2025/6/24 20:0:2组卷：43引用：1难度：0.5
