四边形ABCD是正方形，△BEF是等腰直角三角形，∠BEF=90°，BE=EF．G为DF的中点，连接EG、CG、EC．
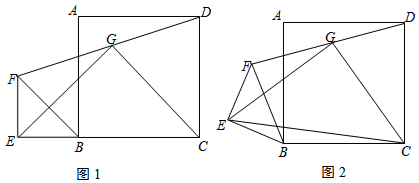
（1）如图，若点E在CB边的延长线上，试判断EG与CG的位置与数量关系，并证明．
（2）将△BEF绕点B顺时针旋转至图2所示位置，请问（1）中所得的结论是否仍然成立？若成立，请写出证明过程．若不成立，请说明理由．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/14 11:0:13组卷：313引用：2难度：0.4
相似题
-
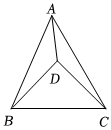1．如图，D是△ABC内一点，∠BDC=90°，BD=CD，AB=20，AC=21，AD=，则BC的长是 ．1322发布：2025/6/14 22:30:1组卷：799引用：3难度：0.5 -
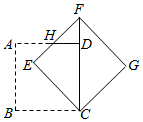2．如图，将边长为1的正方形ABCD绕点C按顺时针方向旋转到FECG的位置，使得点D落在对角线CF上，EF与AD相交于点H，则HD的长为（ ）发布：2025/6/15 1:0:1组卷：144引用：2难度：0.7 -
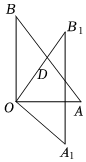3．如图，在△AOB中，∠AOB=90°，OA=3，OB=4．将△AOB绕点O按顺时针方向旋转到△A1OB1处，此时线段OB1与AB的交点D恰好为AB的中点，则B1D的长为（ ）发布：2025/6/14 22:0:2组卷：70引用：2难度：0.6
