如图，在正方形ABCD中，点G为CD边上一点，以CG为边向右作正方形CEFG，连接AF，BD交于点P，连接BG，过点F作FH∥BG交BC于点H，连接PH．
（1）求证：EH=CD；
（2）探究：线段PH和AF的数量关系，说明理由．
【考点】正方形的性质；全等三角形的判定与性质．
【答案】（1）证明过程见解答；
（2）PH=AF．理由见解答．
（2）PH=
1
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/8 8:0:9组卷：346引用：1难度：0.2
相似题
-
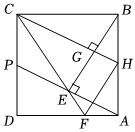1．如图，正方形ABCD的边长为2，P为CD的中点，连接AP，过点B作BE⊥AP于点E，延长CE交AD于点F，过点C作CH⊥BE于点G，交AB于点H，连接HF，则cos∠CEP的值为（ ）发布：2025/6/17 9:0:1组卷：127引用：3难度：0.7 -
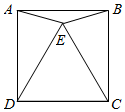2．如图，等边△DEC在正方形ABCD内，连接EA、EB，则∠AEB的度数是．发布：2025/6/17 12:30:1组卷：747引用：6难度：0.8 -
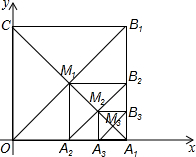3．如图，在平面直角坐标系中，边长为1的正方形OA1B1C的对角线A1C和OB1交于点M1；以M1A1为对角线作第二个正方形A2A1B2M，对角线A1M1和A2B2交于点M2；以M2A1为对角线作第三个正方形A3A1B3M2，对角线A1M2和A3B3交于点M3；…，依此类推，这样作的第6个正方形对角线交点的横坐标为 ．发布：2025/6/17 10:0:1组卷：312引用：6难度：0.7
