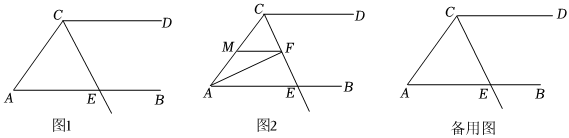
如图1,已知AB∥CD,∠ACD的平分线交AB于点E.
(1)求证:∠ACE=∠AEC;
(2)F为射线CE上一点(不与点C,E重合),连接FA.
①当点F在线段CE上时,如图2,过点F作FM∥AB交AC于点M,当∠ACD=130°,且∠FAB=25°时,求∠AFC的度数;
②当点F在线段CE的延长线上时,探究∠DCF,∠FAB和∠AFC之间的数量关系,并证明你的结论;
③G为线段CE上一点,且∠CAG=3∠EAG,当∠GAF+∠AEC=90°时,直接写出∠CAF∠EAF的值.
∠
CAF
∠
EAF
【考点】平行线的性质.
【答案】(1)证明过程见解答;
(2)①∠AFC的度数为90°;
②∠DCF=∠FAB+∠AFC,理由见解答;
③的值为或5,理由见解答.
(2)①∠AFC的度数为90°;
②∠DCF=∠FAB+∠AFC,理由见解答;
③
∠
CAF
∠
EAF
1
3
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/29 8:0:10组卷:83引用:1难度:0.4