综合与实践：
数学模型可以用来解决一类问题，是数学应用的基本途径．通过探究图形的变化规律，再结合其他数学知识的内在联系，最终可以获得宝贵的数学经验，并将其运用到更广阔的数学天地．
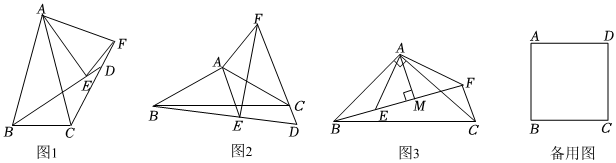
（1）发现问题：如图1，在△ABC和△AEF中，AB=AC，AE=AF，∠BAC=∠EAF=30°，连接BE，CF，延长BE交CF于点D．则BE与CF的数量关系：BE=CFBE=CF，∠BDC=3030°；
（2）类比探究：如图2，在△ABC和△AEF中，AB=AC，AE=AF，∠BAC=∠EAF=120°，连接BE，CF，延长BE，FC交于点D．请猜想BE与CF的数量关系及∠BDC的度数，并说明理由；
（3）拓展延伸：如图3，△ABC和△AEF均为等腰直角三角形，∠BAC=∠EAF=90°，连接BE，CF，且点B，E，F在一条直线上，过点A作AM⊥BF，垂足为点M．则BF，CF，AM之间的数量关系：BF=CF+2AMBF=CF+2AM；
（4）实践应用：正方形ABCD中，AB=2，若平面内存在点P满足∠BPD=90°，PD=1，则S△ABP=7+74或7-747+74或7-74．
7
+
7
4
7
-
7
4
7
+
7
4
7
-
7
4
【答案】BE=CF；30；BF=CF+2AM；或
7
+
7
4
7
-
7
4
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/17 8:0:8组卷：1993引用：6难度：0.5
相似题
-
1．Rt△ABC中，∠ABC=90°，以AB为直径作⊙O交AC边于点D，E是边BC的中点，连接DE，OD．
（Ⅰ）如图①，求∠ODE的大小；
（Ⅱ）如图②，连接OC交DE于点F，若OF=CF，求∠A的大小．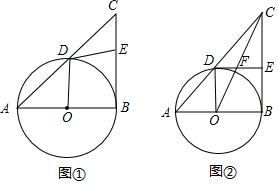
发布：2025/6/18 2:30:1组卷：2269引用：2难度：0.1 -
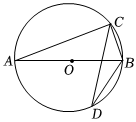2．如图，AB是⊙O的直径，C、D是⊙O上的两点，若∠ABC=70°，则∠BDC的度数为（ ）发布：2025/6/18 9:30:1组卷：594引用：9难度：0.9 -
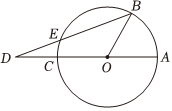3．如图，已知AC是⊙O的直径，点B在圆周上（不与A、C重合），点D在AC的延长线上，连接BD交⊙O于点E，若∠AOB=3∠ADB，则（ ）发布：2025/6/18 6:30:1组卷：4086引用：20难度：0.7
