用火柴棒按如图的方式搭三角形组成的图形．
（1）填写表格：
| 三角形个数 | 1 | 2 | 3 | 4 | 5 | ⋯ |
| 火柴棒根数 | 3 | 5 | 7 |
9 9
|
11 11
|
⋯ |
2n+1
2n+1
（用含n的代数式表示）．（3）是否存在三角形的个数是x由2023根火柴棒拼成？若存在，求出x的值；若不存在，请说明理由．
【考点】规律型：图形的变化类；列代数式．
【答案】9；11；2n+1
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/20 4:0:2组卷：77引用：1难度：0.5
相似题
-
1．如图，在图1中，互不重叠的三角形共有4个，在图2中，互不重叠的三角形共有7个，在图3中，互不重叠的三角形共有10个，…，则在第n个图形中，互不重叠的三角形共有个 （用含n的代数式表示）．
发布：2025/6/17 4:30:1组卷：229引用：48难度：0.7 -
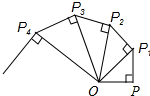2．如图，OP=1，过点P作PP1⊥OP且PP1=1，得OP1=；再过点P1作P1P2⊥OP1且P1P2=1，得OP2=2；又过点P2作P2P3⊥OP2且P2P3=1，得OP3=2…依此法继续作下去，得OP2017=（ ）3发布：2025/6/17 9:30:1组卷：4123引用：15难度：0.7 -
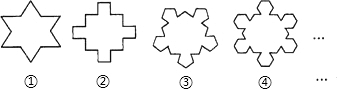
3．如图，①中多边形（边数为12）是由正三角形“扩展”而来的，②中多边形（边数为20）是由正方形“扩展”而来的…．以此类推，由正n边形“扩展”而来的多边形的边为 ．
发布：2025/6/17 5:0:1组卷：134引用：37难度：0.7
