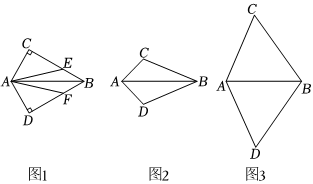
△ABC与△ABD关于直线AB对称，点E，F分别是边BC，BD上的点，且AE=AF．
（1）如图1，若∠C为直角，求证：BE=BF；
（2）若∠C为钝角如图2，∠C为锐角如图3，BE=BF是否还成立？请分别写出你的结论，并选择其中一个结论解答．若成立，请补全图形并证明：若不成立，请画出反例（画反例时保留作图痕迹）．
【考点】轴对称的性质．
【答案】（1）答案见解答过程；
（2）若∠C为钝角时，BE=BF成立，若∠C为锐角时，BE=BF不一定成立，理由见解答过程．
（2）若∠C为钝角时，BE=BF成立，若∠C为锐角时，BE=BF不一定成立，理由见解答过程．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/7 8:0:9组卷：144引用：1难度：0.5
相似题
-
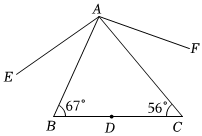1．如图，△ABC中，D点在BC上，将D点分别以AB、AC为对称轴，画出对称点E、F，并连接AE、AF，根据图中标示的角度，∠EAF的度数为（ ）发布：2025/5/22 23:0:1组卷：1023引用：7难度：0.6 -
2．如图，在△ABC中，∠ABC=90°，，BC=8，点D在边BC上，DA=DC，点B关于直线AC的对称点为点E，连接AE、ED，则DE的长为 ．AB=42发布：2025/5/22 23:30:1组卷：129引用：2难度：0.5 -
3．如图，一张矩形ABCD纸片，点P和点Q分别在AD和BC上，沿PQ折叠纸片，点E和点F分别是点D和点C的对应点，如果翻折之后测量得∠BQF=46°，则∠DPQ的度数是 ．发布：2025/5/23 4:0:1组卷：124引用：2难度：0.7
