如图，一人乘雪橇沿坡度为1：3的斜坡笔直滑下，下滑的距离s（米）与时间t（秒）间的关系满足二次函数s=2t2+10t,若滑到坡底的时间为4秒，则此人下降的高度为（ ）
1
：
3
【考点】二次函数的应用；解直角三角形的应用-坡度坡角问题．
【答案】B
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：95引用：2难度：0.9
相似题
-
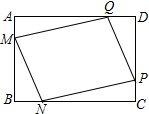1．某小区在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化，为了绿化环境又节省成本．如图，已知矩形的边BC=200m,边AB=a m（a为不大于200的常数），四边形MNPQ的顶点在矩形的边上，且AM=BN=CP=DQ=x m,设四边形MNPQ的面积为S m2
（1）求S关于x的函数关系式，并直接写出自变量x的取值范围；
（2）若a=120，求S的最小值，并求出此时x的值；
（3）若a=200，且每平方米绿化费用需50元，则此时绿化最低费用为万元．发布：2025/6/23 12:30:1组卷：36引用：1难度：0.5 -
2．某公司生产的某种产品每件成本为40元，经市场调查整理出如下信息：
①该产品90天内日销售量（m件）与时间（第x天）满足一次函数关系，部分数据如下表：
②该产品90天内每天的销售价格与时间（第x天）的关系如下表：时间（第x天） 1 3 6 10 … 日销售量（m件） 198 194 188 180 …
（1）求m关于x的一次函数表达式；时间（第x天） 1≤x＜50 50≤x≤90 销售价格（元/件） x+60 100
（2）设销售该产品每天利润为y元，请写出y关于x的函数表达式，并求出在90天内该产品哪天的销售利润最大？最大利润是多少？【提示：每天销售利润=日销售量×（每件销售价格-每件成本）】
（3）在该产品销售的过程中，共有多少天销售利润不低于5400元，请直接写出结果．发布：2025/6/23 11:0:1组卷：2031引用：55难度：0.5 -
3．一公司生产某商品每件成本为20元，经调研发现，该商品在未来40天内的当天销售量m（件）与时间第t（天）满足关系式m=-2t+96；未来40天内，前20天当天的价格y1（元/件）与时间第t（天）的函数式为y1=0.25t+25（1≤t≤20且t为整数），后20天当天的价格y2（元/件）与时间第t（天）的函数式为y2=-0.5t+40（21≤t≤40且t为整数）．
（1）求日销售利润W（元）与时间第t（天）的函数关系式，并写出自变量的取值范围；
（2）请预测未来40天中第 天的日销售利润最大，最大日销售利润是 元．
（3）在实际销售的前20天中，该公司决定每销售一件商品就捐赠a元利润（a＜5）给希望工程，公司通过销售记录发现，前20天中，每天扣除捐赠后的日销售利润随时间第t（天）的增大而增大，求a的取值范围．发布：2025/6/23 11:0:1组卷：116引用：1难度：0.3
