小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展，
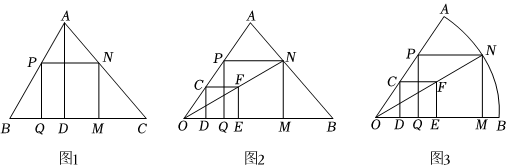
（1）如图1，在△ABC中，AD⊥BC于点D，正方形PQMN的边QM在BC上，顶点P，N分别在AB，AG上，BC=8，AD=4，则正方形PQMN的边长是 125125；
（2）小波继续思考：如何在一个三角形内画出这个正方形PQMN呢？
小波画出了△AOB，然后按数学家波利亚在《怎样解题》中的方法进行操作：如图2，在△AOB内，在AO上任取一点C，画正方形CDEF，使点D，E在OB边上，点F在△AOB内，连接OF并延长交AB于点N，画NM⊥OB于点M，画NP⊥NM交AO于点P，再画PQ⊥OB于点Q，则得到了正方形PQMN．
请你结合图2，依据小波的做法，证明四边形PQMN是正方形；
（3）如图3，在扇形OAB中，小波类比（2）中的作法，又画出了正方形PQMN，若∠AOB=60°，扇形OAB的半径是1，求正方形PQMN的面积．
12
5
12
5
【考点】圆的综合题．
【答案】
12
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/23 8:0:10组卷：47引用：1难度：0.2
相似题
-
1．AB、AC为圆O的弦，OA平分∠BAC．
（1）如图1，求证：弧AB=弧AC；
（2）如图2，连接BO并延长交圆O于点F，连接AF，作BG⊥AC于点G，延长AO交BG于点M，求证：AF=BM；
（3）如图3，在（2）的条件下，连接OG，延长BG交圆O于点D，连接CD并延长，与AF的延长线交于点K，AB=2FK，BC=6，求OG的长．
发布：2025/5/23 16:30:1组卷：112引用：1难度：0.2 -
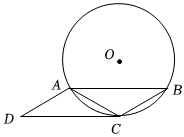2．如图，⊙O是△ABC的外接圆，分别过A，C作AD∥BC，CD∥AB．
（1）求证：AD=BC；
（2）若AC=BC．
①求证：CD是⊙O的切线；
②已知AB=6cm,当四边形ABCD的某条边所在直线过圆心O时，求⊙O的半径．发布：2025/5/23 17:30:1组卷：150引用：2难度：0.1 -
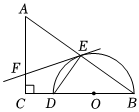3．如图，在△ABC中，∠C=90°，AC=3，BC=4．O为BC边上一点，以O为圆心，OB为半径作半圆，分别于与边BC、AB交于点D、E，连接DE．
（1）∠BED=°；
（2）当BD=3时，求DE的长；
（3）过点E作半圆O的切线，当切线与边AC相交时，设交点为F．求证：AF=EF．发布：2025/5/23 17:30:1组卷：229引用：4难度：0.1
相关试卷
