阅读材料：200多年前，数学王子高斯用他独特的方法快速计算出1+2+3+…+100的值．我们从这个算法中受到启发，用下面方法计算数列1，2，3，…，n,…的前n项和：
由图2可知1+2+3+…+n=（n+1）×n2．
应用以上材料解决下面问题：
（1）有一个三角点阵（如图1），从上向下数有无数多行，其中第一行有1个点，第二行有2个点…，第n行有n个点…，若该三角点阵前n行的点数和为325，求n的值．
（2）在第一问的三角点阵图形中，前n行的点数和能是900吗？如果能，求出n；如果不能，说明理由．
（3）如果把如图1中的三角点阵中各行的点数依次换为3，6，9，…，3n,…，前n行的点数和能是900吗？如果能，求出n；如果不能，说明理由．
1
+
2
+
3
+
…
+
n
=
（
n
+
1
）
×
n
2
【考点】规律型：图形的变化类．
【答案】（1）25；
（2）不能，理由见解析；
（3）能，n=24．
（2）不能，理由见解析；
（3）能，n=24．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/7 8:0:8组卷：117引用：6难度：0.5
相似题
-
1．观察下列等式：13=12，13+23=32，13+23+33=62，13+23+33+43=102，…，想一想：等式左边各个幂的底数与右边幂的底数有什么关系，并用等式表示出规律；再利用这一规律计算13+23+33+43+…+1003的值．
发布：2025/6/18 9:30:1组卷：226引用：4难度：0.3 -
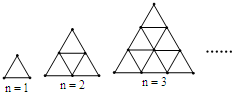2．如图，是用火柴棍摆出的一系列三角形图案，按这种方式摆下去，当每边摆上20（n=20）根时，需火柴棍为根，若当每边摆上n根时，试写出需火柴棍为根．发布：2025/6/18 11:0:1组卷：161引用：1难度：0.7 -
3．如图所示，用火柴杆摆出一系列三角形图案，共摆有n层，当n=1时，需3根火柴；当n=2时，需9根火柴，按这种方式摆下去，
（1）当n=3时，需根火柴．
（2）当n=10时，需根火柴．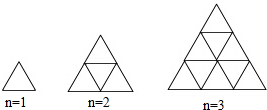
发布：2025/6/18 11:30:2组卷：106引用：1难度：0.5
