某数学兴趣小组在活动时，老师提出了这样一个问题：如图1，在△ABC中，AB=6，AC=8，D是BC的中点，求BC边上的中线AD的取值范围．
小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使DE=AD，请补充完整证明“△ABD≌△ECD”的推理过程．
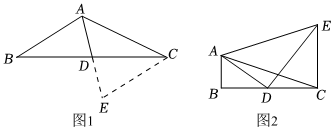
（1）求证：△ABD≌△ECD；
证明：延长AD到点E，使DE=AD，
在△ABD和△ECD中，
∴AD=ED（已作），
∠ADB=∠EDC（ 对顶角相等对顶角相等），
CD=BDBD（中点定义），
∴△ABD≌△ECD（ SASSAS）．
（2）由（1）的结论，根据AD与AE之间的关系，探究得出AD的取值范围是 1＜AD＜71＜AD＜7；
（3）【感悟】解题时，条件中若出现“中点”“中线”等字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．
【问题解决】如图2中，∠B=90°，AB=2，AD是△ABC的中线，CE⊥BC，CE=4，且∠ADE=90°，求AE的长．
【考点】三角形综合题．
【答案】对顶角相等；BD；SAS；1＜AD＜7
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/31 15:0:9组卷：182引用：4难度：0.3
相似题
-
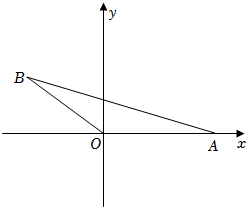1．如图，在平面直角坐标系中，点O为坐标原点，点A（6，0），B（m,n），其中m,n满足，连接AB、OB．2m-n=-113m+5n=3
（1）求点B的坐标．
（2）动点P以每秒2个单位长度的速度从点O出发，沿y轴正半轴匀速运动，设点P运动时间为t秒，请用含t的式子表示△ABP的面积．
（3）在（2）的条件下，在y轴负半轴取一点C，CP=10，点D是△AOP内部一点，连接PD、CD，CD与x轴交点F坐标（1，0），连接AD并延长交OP于点E，若∠EDP=45°，∠DEC=2∠EPD+∠ECD，当时，求点P的坐标．CF•AD=1031S△ABP发布：2025/6/8 22:0:1组卷：144引用：1难度：0.3 -
2．在△ABC中，∠BAC=90°，AB=AC，点P为AC上一点，点M为BC上一点，线段AM，BP交于点E．
（1）若BP为△ABC的角平分线．
①如图1，已知AM⊥BC，求证：AE=AP；
②如图2，已知AM⊥BP，求证：AP=PM；
（2）如图3，若BP为△ABC的中线，且AM⊥BP，试探究BP，AM，MP三条线段的数量关系是 （直接写出答案）．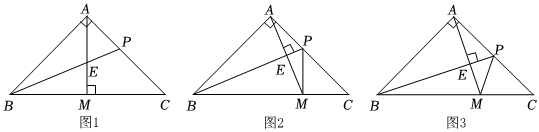
发布：2025/6/8 22:0:1组卷：90引用：3难度：0.3 -
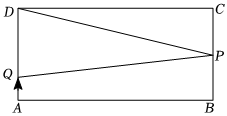3．如图，在长方形ABCD中，AB=8，AD=4．P是BC的中点，点Q从点A出发，以每秒2个单位长度的速度沿A→D→C→B→A的方向向终点A运动，设点Q运动的时间为x秒．
（1）点Q在运动的路线上和点C之间的距离为4时，x=秒．
（2）若△DPQ的面积为S，用含x的代数式表示S（0≤x＜7）．
（3）若点Q从A出发3秒后，点M以每秒6个单位长度的速度沿A→B→C→D的方向运动，M点运动到达D点后立即沿着原路原速返回到A点，当M与Q在运动的路线上相距不超过4时，请直接写出相应x的取值范围．发布：2025/6/8 18:0:1组卷：139引用：1难度：0.2
