阅读与思考
如图1，在△ABC中，AD平分∠BAC，EF垂直平分AD交BC的延长线于点F，求证：DF2=BF•CF．
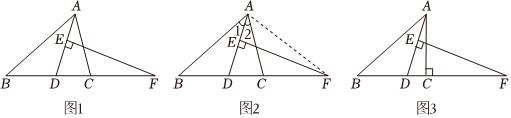
（1）任务1，如图2，下面是小明的证明过程，请你补充完整并填写依据．
证明：连接AF，
∵AD平分∠BAC，
∴∠1=∠2，
∵EF垂直平分AD，
∴AFAF=DFDF（依据1：垂直平分线的性质垂直平分线的性质），
∴∠ADF=∠DAF，
∵∠ADF=∠1+∠B，∠DAF=∠2+∠CAF，
∴∠B∠B=∠CAF∠CAF，
∵∠AFB∠AFB=∠CFA∠CFA，
∴△ABF∽△CAF（依据2：有两组角分别相等的两个三角形相似有两组角分别相等的两个三角形相似），
∴AFCE=BFAF，
∴AF2=BF•CF，
∵FA=FD，
∴DF2=BF•CF．
（2）任务2，如图3，当∠ACB=90°时，其它条件不变，若BF=9，CF=4，则AC=2525．
AF
CE
=
BF
AF
5
5
【考点】相似三角形的判定与性质；线段垂直平分线的性质．
【答案】AF；DF；垂直平分线的性质；∠B；∠CAF；∠AFB；∠CFA；有两组角分别相等的两个三角形相似；2
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/27 7:0:8组卷：27引用：1难度：0.5
相似题
-
1．如图，梯形ABCD中AD∥BC，对角线AC、BD交于0点，△AOD与△DOC的面积之比为3：7，则AD：BC=．发布：2025/1/28 8:0:2组卷：39引用：1难度：0.7 -
2．如图，在梯形ABCD中，AB∥CD，对角线AC、BD相交于点O，如果S△AOB=2S△AOD，AC=10，那么OC的长是．发布：2025/1/28 8:0:2组卷：107引用：1难度：0.4 -
3．如图，AB是圆O的直径，C是半径OB的中点，D是OB延长线上一点，且BD=OB，直线MD与圆O相交于点M、T（不与A、B重合），DN与圆O相切于点N，连接MC，MB，OT．
（Ⅰ）求证：DT•DM=DO•DC；
（Ⅱ）若∠DOT=60°，试求∠BMC的大小．发布：2025/1/28 8:0:2组卷：364引用：1难度：0.3
