为了安全起见，在某条河流的两岸各安置了一应旋转探照灯．如图1所示，灯A的光线从AM开始顺时针旋转至AN便立即回转，灯B的光线从BP开始顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视．若灯A转动的速度是每秒3度，灯B转动的速度是每秒2度．假定这段河流的两岸是平行的，即PQ∥MN，且∠BAM：∠ABQ=3：1．

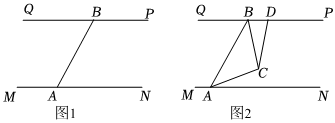
（1）求∠BAN的度数；
（2）如果灯B的光线先转动5秒，灯A的光线才开始转动，那么在灯B的光线到达BQ之前，灯A转动几秒时，两灯的光束互相平行？
（3）如图2，两灯同时转动，在灯A的光线到达AN之前，若两灯射出的光束交于点C，过C作∠ACD=135°，CD交PQ于点D，则在转动过程中，探究∠BAC与∠BCD的数量关系是否发生变化？若不变，请用等式表示出它们之间的数量关系；若改变，请说明理由．