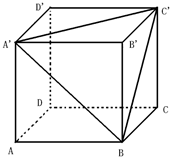
如图，已知正方体ABCD-A'B'C'D'的棱长为1.
（1）求异面直线BA′与CC′所成角的度数；
（2）求三棱锥B′-A′BC′的体积.
解：（1）在正方体ABCD-A'B'C'D'中
∵C′C ∥∥B′B
∴∠B'BA'等于异面直线BA′与CC′的夹角
∴BA′与CC′所成的角等于 45°45°
（2）三棱锥B′-A′BC′的体积等于三棱锥C′-A′B′B的体积
∵A′B′=B′B=C′B′=1
∴三棱锥B′-A′BC′的体积等于 1616
1
6
1
6
【答案】∥；45°；
1
6
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：11引用：1难度：0.8
