根据以下素材，探索完成任务．

如何设计警戒线之间的宽度？

素材1
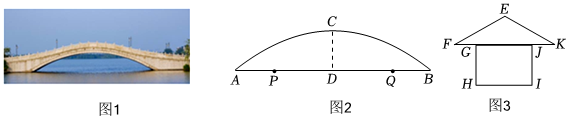
图1为某公园的抛物线型拱桥，图2是其横截面示意图，测得水面宽度AB=24米，拱顶离水面的距离为CD=4米．

素材2 拟在公园里投放游船供游客乘坐，载重最少时，游船的横截面如图3所示，漏出水面的船身为矩形，船顶为等腰三角形．如图3，测得相关数据如下：EF=EK=1.7米，FK=3米，GH=IJ=1.26米，FG=JK=0.4米．

素材3 为确保安全，拟在石拱桥下面的P，Q两处设置航行警戒线，要求如下：
①游船底部HI在P，Q之间通行；
②当载重最少通过时，游船顶部E与拱桥的竖直距离至少为0.5米．

问题解决

任务1 确定拱桥形状在图2中建立合适的直角坐标系，并求这条抛物线的函数表达式．

任务2 设计警戒线之间的宽度求PQ的最大值．

【答案】任务1：y=-

x²+4；
任务2：PQ的最大值为16.6米．

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/10/2 6:0:2组卷：860引用：9难度：0.5

相似题

1．在一定条件下，若物体运动的路程s（米）与时间t（秒）的关系式为s=5t²+2t,则当物体经过的路程是88米时，该物体所经过的时间为（　　）
A．2秒 B．4秒 C．6秒 D．8秒
发布：2025/6/17 20:30:2组卷：288引用：2难度：0.5
解析

2．我市某乡镇在“精准扶贫”活动中销售一农产品，经分析发现月销售量y（万件）与月份x（月）的关系为：y=
x
+
4
（
1
≤
x
≤
8
，
x
为整数
）
-
x
+
20
（
9
≤
x
≤
12
，
x
为整数
）
，每件产品的利润z（元）与月份x（月）的关系如下表：

x 1 2 3 4 5 6 7 8 9 10 11 12

z 19 18 17 16 15 14 13 12 11 10 10 10

（1）请你根据表格求出每件产品利润z（元）与月份x（月）的关系式；
（2）若月利润w（万元）=当月销售量y（万件）×当月每件产品的利润z（元），求月利润w（万元）与月份x（月）的关系式；
（3）当x为何值时，月利润w有最大值，最大值为多少？

发布：2025/6/18 0:0:2组卷：2248引用：12难度：0.3

如何设计警戒线之间的宽度？
素材1	图1为某公园的抛物线型拱桥，图2是其横截面示意图，测得水面宽度AB=24米，拱顶离水面的距离为CD=4米．
素材2	拟在公园里投放游船供游客乘坐，载重最少时，游船的横截面如图3所示，漏出水面的船身为矩形，船顶为等腰三角形．如图3，测得相关数据如下：EF=EK=1.7米，FK=3米，GH=IJ=1.26米，FG=JK=0.4米．
素材3	为确保安全，拟在石拱桥下面的P，Q两处设置航行警戒线，要求如下： ①游船底部HI在P，Q之间通行； ②当载重最少通过时，游船顶部E与拱桥的竖直距离至少为0.5米．
问题解决
任务1	确定拱桥形状	在图2中建立合适的直角坐标系，并求这条抛物线的函数表达式．
任务2	设计警戒线之间的宽度	求PQ的最大值．