如图1，已知直线EF与直线AB交于点E，直线EF与直线CD交于点F，EM平分∠AEF交直线CD于点M，且∠FEM=∠EMF．
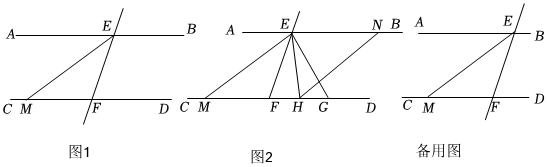
（1）求证：AB∥CD；
（2）点G是射线MD上的一个动点（不与点M、F重合），EH平分∠FEG交直线CD于点H，过点H作HN∥EM交直线AB于点N，设∠EHN=α，∠EGF=β．
①如图2，当点G在点F的右侧时，若β=80°，求α的值，并说明理由；
②当点G在运动过程中，α和β之间有怎样的数量关系？直接写出你的结论．
【考点】平行线的判定与性质．
【答案】（1）见解析；（2）①α=50°，理由见解析；②α和β之间的数量关系是：或．
α
+
1
2
β
=
90
°
α
=
1
2
β
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/29 8:0:10组卷：198引用：3难度：0.4
相似题
-
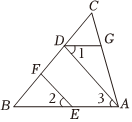1．推理填空：
如图，EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．
因为EF∥AD，
所以∠2=．（ ）
又因为∠1=∠2，
所以∠1=∠3．（ ）
所以AB∥．（ ）
所以∠BAC+=180°（ ）
又因为∠BAC=70°，
所以∠AGD=．发布：2025/6/18 7:0:1组卷：1131引用：35难度：0.7 -
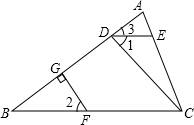2．如图，在△ABC中，∠1=∠2，∠3=∠B，FG⊥AB于G，猜想CD与AB的位置关系，并证明你的猜想．发布：2025/6/18 12:30:1组卷：167引用：5难度：0.7 -
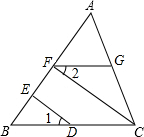3．如图，∠1=∠2，CF⊥AB，DE⊥AB，求证：FG∥BC．发布：2025/6/18 17:0:1组卷：685引用：8难度：0.3
