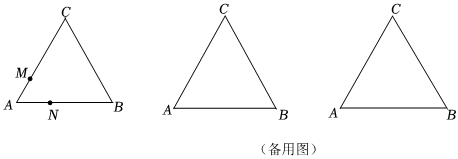
如图，△ABC中，AB=BC=AC=6cm,点M、N分别从点A、点B同时出发，沿三角形的边顺时针运动，点M的速度为2cm/s,点N的速度为3cm/s,当点M，点N第一次相遇时，点M，点N同时停止运动，设点M，点N的运动时间为t（t＞0）秒．
（1）当t=2时，CM=2cm2cm；当t=5时，CM=4cm4cm．
（2）当点N在AC上时，CN=12-3t12-3t；当点N在CB上时，CN=3t-123t-12（分别用含t的代数式表示）．
（3）点N在CB上时，若△AMN为直角三角形时，直接写出t的值．
（4）连结MN，当线段MN的垂直平分线经过△ABC的某一顶点时，直接写出t的值．
【考点】三角形综合题．
【答案】2cm；4cm；12-3t；3t-12
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/29 2:0:8组卷：124引用：4难度：0.3
相似题
-
1．如图1，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，动点P在线段BC上，点Q在线段AB上，且PQ=BQ，延长QP交射线AC于点D．
（1）求证：QA=QD；
（2）设∠BAP=α，当2tanα是正整数时，求PC的长；
（3）作点Q关于AC的对称点Q′，连接QQ′，AQ′，DQ′，延长BC交线段DQ′于点E，连接AE，QQ′分别与AP，AE交于点M，N（如图2所示）．若存在常数k,满足k•MN=PE•QQ′，求k的值．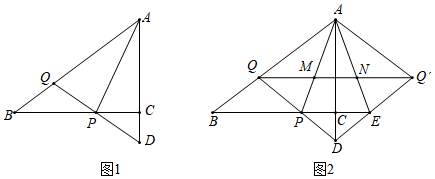
发布：2025/6/16 4:0:2组卷：233引用：3难度：0.2 -
2．在△ABC中，∠ACB=2∠B．
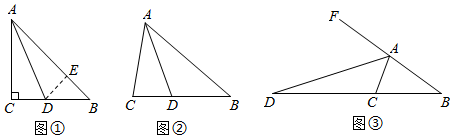
（1）如图①，当∠C=90°，AD为∠BAC的角平分线时，在AB上截取AE=AC，连接DE，易证：CD=DE=；AC+CD=；（请直接写出结论，不用证明．）
（2）如图②，当∠C≠90°，AD为∠BAC的角平分线时，模仿题（1）的思路，求证：AB=AC+CD；
（3）如图③，当AD为△ABC的外角平分线时，线段AB，AC，CD又有怎样的数量关系？请写出你的猜想，并对你的猜想给予证明．发布：2025/6/16 18:30:2组卷：191引用：1难度：0.4 -
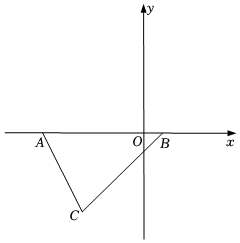3．如图，在平面直角坐标系中，A（a,0），B（b,0），且满足，C在第三象限，坐标为（n+1，n），连接AC，BC，（a+5）2+b-1=0
（1）请直接写出：a=，b=，AB=，S△ABC=（用含n的代数式表示）；
（2）在线段AB上取一点D，连接CD并延长，交y轴于点E，连接AE，BE，
①若S△DCA=2S△DEA，求点E坐标，用含n的代数式表示．
②若S△ADC=S△DBE，求点E坐标．发布：2025/6/15 14:0:2组卷：144引用：1难度：0.1
