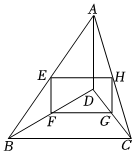
阅读理解：已知三角形的中线具有等分三角形面积的性质，即如图①，AD是△ABC中BC边上的中线，则S_△ABD=S_△ACD=

1

2

S

△

ABC

，理由：∵BD=CD，∴S_△ABD=

1

2

BD，AH=

1

2

CD

⋅

AH

=

S

△

ACD

=

1

2

S

△

ABC

，即：等底同高的三角形面积相等．

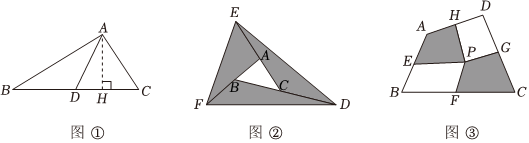
回答下列问题：（1）如图②，点A、B、C分别是CE、AF、BD的中点，且S_△ABC=2，则图②中阴影部分的面积为

12

12

；
（2）如图③，已知四边形ABCD的面积是m,E、F、G、H分别是AB、BC、CD、DA的中点，点P是四边形ABCD内一点，求出图中阴影部分的面积．