2023年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本2500万元.每生产x(百辆)新能源汽车,需另投入成本C(x)万元,且C(x)=10x2+100x, 0<x<40 501x+10000x-4500, x≥40
.由市场调研知,每辆车售价5万元,且生产的车辆当年能全部销售完.
(1)求出2023年的利润L(x)(万元)关于年产量x(百辆)的函数关系式.(利润=销售额-成本)
(2)2023年产量为多少百辆时,企业所获利润最大?并求出最大利润.
C
(
x
)
=
10 x 2 + 100 x , | 0 < x < 40 |
501 x + 10000 x - 4500 , | x ≥ 40 |
【考点】从实际问题中抽象出函数模型.
【答案】(1)
;(2)2023年产量为100百辆时利润最大,最大利润为1800万元.
L
(
x
)
=
- 10 x 2 + 400 x - 2500 , | 0 < x < 40 |
2000 - ( x + 10000 x ) , | x ≥ 40 |
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/10/19 0:0:1组卷:36引用:3难度:0.5
相似题
-
1.某礼品店要制作一批长方体包装盒,材料是边长为60cm的正方形纸板.如图所示,先在其中相邻两个角处各切去一个边长是xcm的正方形,然后在余下两个角处各切去一个长、宽分别为30cm、xcm的矩形,再将剩余部分沿图中的虚线折起,做成一个有盖的长方体包装盒.
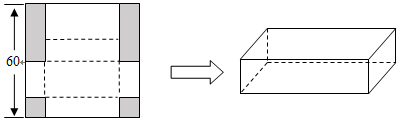
(1)求包装盒的容积V(x)关于x的函数表达式,并求函数的定义域;
(2)当x为多少时,包装盒的容积最大?最大容积是多少?发布:2025/1/2 22:0:1组卷:2引用:1难度:0.5 -
2.某城市2018年底人口总数为50万,绿化面积为35万平方米.假定今后每年人口总数比上-年增加1.5万,每年新增绿化面积是上一年年底绿化面积的5%,并且每年均损失0.1万平方米的绿化面积(不考虑其他因素).
(l)到哪一年年底,该城市人口总数达到60万(精确到1年)?
(2)假如在人口总数达到60万并保持平稳、不增不减的情况下,到哪一年年底,该城市人均绿化面积达到0.9平方米(精确到1年)?发布:2025/1/2 22:0:1组卷:23引用:2难度:0.5 -
3.某书店主要销售中职类教辅资料,现有一款2023版中职数学教辅资料,进价为每本14元,出版社规定该资料的售价不能低于进价.书店老板将该教辅资料的售价定为每本26元进行销售,每月可实出80本.销售主管小张发现:该教辅资料的售价每降价1元,每月的销量将增加10本.则该款教辅资料定价为
元时,月销售利润最大.发布:2025/1/2 22:0:1组卷:10引用:1难度:0.7


