教育部印发《义务教育课程方案》和课程标准（2022年版），将劳动从原来的综合实践活动课程中独立出来．某中学为了让学生体验农耕劳动，如图（1）在正方形绿化带ABCD内修建一个矩形耕种园AEFG，其中点G在AD上，点E在AB上，已知正方形绿化带ABCD的面积为400m2，AB，AD是墙壁，BC，CD无墙壁．
已知矩形耕种园AEFG的面积为正方形花园面积的14，该耕种园借助绿化带的墙壁，只设置围栏GF，EF即可．小明用所学的数学知识进行了如下探究．
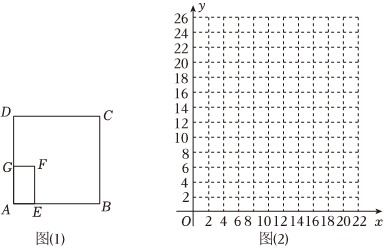
（1）建立数学模型
由题意知，此耕种园的面积为400×14=100（m2），设AE=x米，则AG=100x米．设所需围栏的长度为y米，则y关于x的函数解析式为 y=100x+xy=100x+x．
（2）画出函数图象
①列表：
1
4
400
×
1
4
=
100
（
m
2
）
AG
=
100
x
y
=
100
x
+
x
y
=
100
x
+
x
| x | 5 | 8 | 10 | 12.5 | 16 | 20 |
| y | 25 | 20.5 | 20 | 20.5 | 22.25 | a |
25
25
．②请根据上表数据，在如图（2）所示的平面直角坐标系中描点，并画出y关于x的函数图象，其中，自变量x的取值范围是
5≤x≤20
5≤x≤20
．（3）观察函数图象，解决问题
①当所用围栏最短时，AG的长为
10
10
米．②若学校打算用20.5米的围栏建设耕种园（围栏正好用完），则AG=
12.5或8
12.5或8
米．③若围栏的长度为b米，则b的取值范围为
20＜b≤25
20＜b≤25
时，每一个b值都对应两种围栏方式．【考点】四边形综合题．
【答案】；25；5≤x≤20；10；12.5或8；20＜b≤25
y
=
100
x
+
x
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/13 8:0:9组卷：60引用：2难度：0.2
相似题
-
1．如图1，点E为正方形ABCD内一点，∠AEB=90°，现将Rt△ABE绕点B按顺时针方向旋转90°，得到△CBE′（点A的对应点为点C），延长AE交CE′于点F．
（1）如图1，求证：四边形BEFE′是正方形；
（2）连接DE，
①如图2，若DA=DE，求证：F为CE′的中点；
②如图3，若AB=15，CF=3，试求DE的长．发布：2025/6/8 22:30:1组卷：532引用：2难度：0.4 -
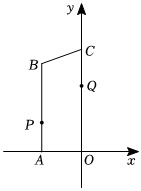2．如图在平面直角坐标系中，A（-8，0），C（0，26），AB∥y轴且AB=24，点P从点A出发，以1个单位长度/s的速度向点B运动；点Q从点C同时出发，以2个单位长度/s的速度向点O运动，规定其中一个动点到达端点时，另一个动点也随之停止运动，设运动的时间为t秒．
（1）当四边形BCQP是平行四边形时，求t的值；
（2）当PQ=BC时，求t的值；
（3）当PQ恰好垂直平分BO时，求t的值．发布：2025/6/8 22:30:1组卷：177引用：3难度：0.3 -
3．在△ABC中，∠ACB为锐角，点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．解答下列问题：
（1）如果AB=AC，∠BAC=90°，
①如图1，当点D在线段BC上时（与点B不重合），线段CF、BD之间的位置关系为 ；数量关系为 ．
②如图2，当点D在线段BC的延长线上时，①中的结论是否仍然成立，并说明理由．
（2）如图3，如果AB＜AC，∠BAC＜90°，点D在线段BC上运动（与点B不重合）．
试探究：当∠ACB=45°时，（1）中的CF，BD之间的位置关系是否仍然成立，并说明理由．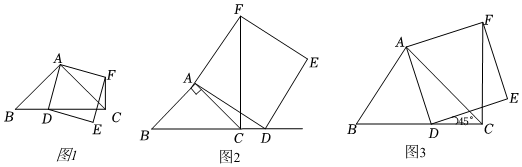
发布：2025/6/8 20:30:2组卷：161引用：3难度：0.3
