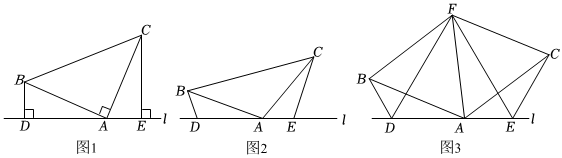
（1）某学习小组在探究三角形全等时，发现了下面这种典型的基本图形．如图1，在△ABC中，∠BAC=90°，AB=CA，直线l经过点A，作BD⊥直线l,CE⊥直线l,垂足分别为点D，E．请说明DE=BD+CE．
（2）组员小明想，如果三个相等的角不是直角，那么（1）中的结论是否会成立呢？如图2，将（1）中的条件改为：在△ABC中，AB=CA，D，A，E三点都在直线l上，且∠BDA=∠AEC=∠BAC．请判断DE=BD+CE是否成立，并说明理由．
（3）数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题．如图3，D，E是直线l上的两动点（D，A，E三点均在直线l上且互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD，CE．若∠BDA=∠AEC=∠BAC，请说明DF=EF．
【考点】三角形综合题．
【答案】（1）证明见解答过程；
（2）DE=BD+CE成立，理由见解答过程；
（3）证明见解答过程．
（2）DE=BD+CE成立，理由见解答过程；
（3）证明见解答过程．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/17 8:0:9组卷：151引用：5难度：0.5
相似题
-
1．如图，△ABC中，CA=CB、∠ACB=α，过点B作直线l∥AC，D为线段AB上一动点，连接CD，将射线DC绕点D顺时针旋转α，交直线l于点E．
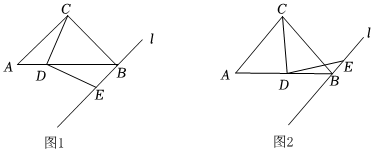
（1）如图1，当α=90°时，线段CD和ED的数量关系是 ．
（2）如图2，当0°＜α＜180°时，（1）中的结论是否仍然成立？若成立，请仅就图2的情形给出证明；若不成立，请说明理由．
（3）若α=120°，AC=，当△DEB为直角三角形时，请直接写出线段DE的长．3发布：2025/5/24 1:30:2组卷：55引用：1难度：0.1 -
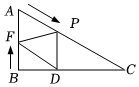2．如图，在Rt△ABC中，∠ABC=90°，∠C=30°，AB=9cm，动点P从点A开始以2cm/s的速度向点C运动，动点F从点B开始以1cm/s的速度向点A运动，两点同时运动，同时停止，运动时间为t（s）．
（1）当t为何值时，△PAF是等边三角形？
（2）当t为何值时，△PAF是直角三角形？
（3）过点P作PD⊥BC于点D，连接DF．
①求证：四边形AFDP是平行四边形；
②当t为何值时，△PDC的面积是△ABC面积的一半．发布：2025/5/24 1:0:1组卷：283引用：3难度：0.3 -
3．在一次数学兴趣小组活动中，小明将两个形状相同，大小不同的三角板AOB和三角板DEB放置在平面直角坐标系中，点O（0，0），A（0，3），∠ABO=30°，BE=3．
（Ⅰ）如图①，求点D的坐标；
（Ⅱ）如图②，小明同学将三角板DEB绕点B按顺时针方向旋转一周．
①若点O，E，D在同一条直线上，求点D到x轴的距离；
②连接DO，取DO的中点G，在旋转过程中，点G到直线AB的距离的最大值是 （直接写出结果即可）．发布：2025/5/24 1:0:1组卷：573引用：2难度：0.3
