【问题提出】有编号分别为1，2，3，…，n（n为正整数，且n≥1）的n个球，甲、乙轮流抓，每次可以抓1个球或相连编号的2个球．甲先抓，规定谁抓到最后一次谁获胜．甲第1次应该怎样抓才能获胜？
【问题探究】我们采取一般问题特殊化的策略，先从最简单的情形入手，再逐次递进，从中找规律．
（1）如图①，当n=1时，甲一次抓一个球就可以抓完，显然甲获胜；
（2）如图②，当n=2时，甲一次抓编号相连的1号和2号2个球就可以抓完，所以甲获胜；
（3）如图③，当n=3时，甲第1次先抓2号球，乙第1次无论抓1号球还是3号球，最后还剩1个球，甲第2次抓就可以抓完，所以甲获胜；
（4）如图④，当n=4时，甲第1次先抓编号相连的2号和3号球，乙第1次无论抓1号球还是4号球，最后还剩1个球，甲第2次抓就可以抓完，所以甲获胜；
（5）如图⑤，当n=5时，甲第1次先抓3号球，乙第1次抓有两类抓法：一类：一次抓1个球．若乙第1次从1号和2号中任抓1个球，则甲第2次从4号和5号中任抓1个球，乙第2次无论抓那个球，最后还剩1个球，甲第3次抓就可以抓完，甲获胜．同理，若乙第1次从4号和5号中任抓1个球，甲也会获胜．二类：一次抓相连编号的2个球．若乙第1次抓编号相连的1号和2号球，则甲第2次抓编号相连的4号和5号球就可以抓完，甲获胜．同理，若乙第1次抓编号相连的4号和5号球，甲也会获胜．
（6）如图⑥，当n=6时，甲第1次应该怎样抓第1次应该抓 3号球和4号球3号球和4号球号球；
（7）如图⑦，当n=7时，甲要获胜，第1次应该抓 4号球4号球号球；
【问题解决】有编号分别为1，2，3，…，n（n为正整数，且n≥1）的n个球，甲、乙轮流抓，每次可以抓1个球或相连编号的2个球．甲先抓，规定谁抓到最后一次谁获胜．甲第1次应该怎样抓才能获胜？（只写出结论）
【拓展应用】有编号分别为1，2，3，…，（n为正整数，且n≥1）的n个球，甲、乙轮流抓，每次可以抓1个球或相连编号的2个球．甲先抓，规定谁抓到最后一次谁获胜．若甲第1次抓2023号球，最后甲获胜，则n=40474047．
【考点】规律型：图形的变化类．
【答案】3号球和4号球；4号球；4047
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/8 3:0:1组卷：109引用：1难度：0.7
相似题
-
1．某城市大剧院地面的一部分为扇形，观众席的座位按下列方式设置：
上述问题中，第五排、第六排分别有 个、个座位；第n排有 个座位．排数 1 2 3 4 … 座位数 50 53 56 59 … 发布：2025/6/15 5:0:1组卷：37引用：3难度：0.6 -
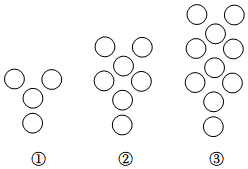2．下列图形都是由同样大小的圆按照一定规律所组成的，其中第①个图形中一共有4个圆，第②个图形中一共有7个圆，第③个图形中一共有10个圆，…，照此规律下去，则第7个图形中圆的个数为（ ）发布：2025/6/14 18:30:4组卷：193引用：3难度：0.7 -
3．如图所示，下列图形都是由相同的玫瑰花按照一定的规律摆成的，按此规律摆下去，第n个图形中有120朵玫瑰花，则n的值为 ．
发布：2025/6/14 21:0:1组卷：188引用：4难度：0.6
