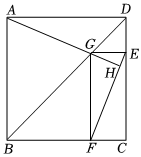
如图，在正方形ABCD中，G是对角线BD上的一点（与点B，D不重合），GE⊥CD，GF⊥BC，E，F分别为垂足．连接EF，AG，并延长AG交EF于点H．
（1）求证：∠DAG=∠EGH；
（2）判断AH与EF是否垂直，并说明理由．
【答案】见解答．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/8 8:0:8组卷：3886引用：8难度：0.5
相似题
-
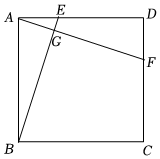1．如图，正方形ABCD中，点E，F分别在AD，CD上，且AF⊥BE于G，连接BE，AF．求证：BE=AF．发布：2025/5/23 23:30:1组卷：332引用：4难度：0.6 -
2．如图①，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM．
（1）连接MN，△BMN是等边三角形吗？为什么？
（2）求证：△AMB≌△ENB；
（3）①当M点在何处时，AM+CM的值最小；
②如图②，当M点在何处时，AM+BM+CM的值最小，请你画出图形，并说明理由．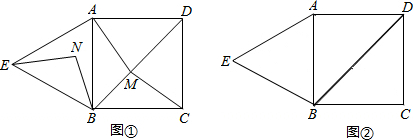
发布：2025/5/23 23:30:1组卷：2860引用：10难度：0.3 -
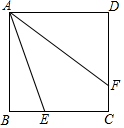3．已知正方形ABCD的边长为2，E，F分别是边BC，CD上的两个动点，且满足BE=CF，连接AE，AF，则AE+AF的最小值为 ．发布：2025/5/23 23:30:1组卷：1298引用：3难度：0.7
