如图（1），是两个全等的直角三角形（直角边分别为a,b,斜边为c）．
（1）用这样的两个三角形构造成如图（2）的图形，利用这个图形，可以证明我们学过的哪个定理，用字母表示：c2=a2+b2c2=a2+b2；
（2）如图（3），当a=3，b=4时，将其中一个直角三角形放入平面直角坐标系中，使直角顶点与原点重合，两直角边a,b分别与x轴、y轴重合（如图4中Rt△AOB的位置）．点C为线段OA上一点，将△ABC沿着直线BC翻折，点A恰好落在x轴上的D处．
①请写出C、D两点的坐标；
②若△CMD为等腰三角形，点M在x轴上，请直接写出符合条件的所有点M的坐标．
【考点】三角形综合题．
【答案】c2=a2+b2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/14 7:0:10组卷：193引用：4难度：0.3
相似题
-
1．如图，三角形ABO的三个顶点的坐标分别为O（0，0），A（5，0），B（2，4）．
（1）求三角形OAB的面积；
（2）若O，B两点的位置不变，点M在x轴上，则点M在什么位置时，三角形OBM的面积是三角形OAB的面积的2倍？
（3）若O，A两点的位置不变，点N由点B向上或向下平移得到，则点N在什么位置时，三角形OAN的面积是三角形OAB的面积的2倍？发布：2025/6/17 6:30:2组卷：331引用：2难度：0.3 -
2．已知a,b,c是△ABC的三边长，a=4，b=6，设三角形的周长是x.
（1）直接写出c及x的取值范围；
（2）若x是大于14的偶数．
①求c的长；
②判断△ABC的形状．发布：2025/6/16 22:30:4组卷：117引用：2难度：0.4 -
3．如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．
（1）求证：AD=BE；
（2）求∠AEB的度数；
（3）探究：如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D，E在同一直线上，CM⊥DE于点M，连接BE．
①∠AEB的度数为 °；
②线段DM，AE，BE之间的数量关系为 ．（直接写出答案，不需要说明理由）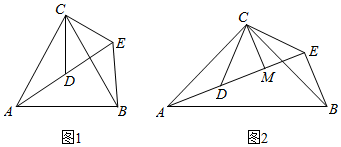
发布：2025/6/17 6:0:2组卷：365引用：3难度：0.6
