 在函数的学习过程中,我们经历“画函数图象一利用函数图象研究其性质一运用函数图象解决问题”的学习过程.
在函数的学习过程中,我们经历“画函数图象一利用函数图象研究其性质一运用函数图象解决问题”的学习过程.
下面根据学习函数的过程和方法,探究分段函数y==x2+4x-1(x≤1) 4x-5(x>1)
的相关性质和应用.
(1)在如图所示的平面直角坐标系中,画出了分段函数图象的一部分,补全该分段函数的图象.
x 2 + 4 x - 1 ( x ≤ 1 ) |
4 x - 5 ( x > 1 ) |
| x | …… | -5 | -4 | -3 | -2 | -1 | 0 | 1 |
| y | …… | 4 | -1 | -4 | -5 | -4 | -1 | 4 |
当x>1时,y随x的增大而增大(答案为唯一)
当x>1时,y随x的增大而增大(答案为唯一)
;(2)直线y=k与该分段函数的图象有2个交点,则k的取值范围是
-1≤k≤4或k=-5
-1≤k≤4或k=-5
;(3)若该分段函数图象上有两点A(-3,y1)B(m,y2),且y1<y2,则m的取值范围是
m<-1或-1<m<4
m<-1或-1<m<4
;(4)当x≥a时,函数值y的取值范围为-5≤y≤b,当a取某个范围内的任意值时,b为定值,直接写出满足条件的a的取值范围及其对应的b值.
【考点】函数的图象.
【答案】当x>1时,y随x的增大而增大(答案为唯一);-1≤k≤4或k=-5;m<-1或-1<m<4
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/12 16:0:8组卷:103引用:2难度:0.5
相似题
-
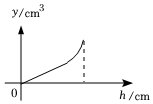 1.容器高为30cm,现向容器内注水,直到注满为止.若容器内的注水量y(cm3)与容器内的水深h(cm)之间的变化关系的图象大致如图所示,则这个容器的形状可能是( )发布:2025/6/20 11:0:1组卷:63引用:1难度:0.7
1.容器高为30cm,现向容器内注水,直到注满为止.若容器内的注水量y(cm3)与容器内的水深h(cm)之间的变化关系的图象大致如图所示,则这个容器的形状可能是( )发布:2025/6/20 11:0:1组卷:63引用:1难度:0.7 -
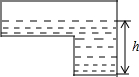 2.如图,是蓄水池的横断面示意图,分深水区和浅水区,如果以固定的流量向蓄水池注水,下面哪个图象能大致表示水的最大深度h和时间t之间的关系( )发布:2025/6/20 12:0:2组卷:1450引用:9难度:0.7
2.如图,是蓄水池的横断面示意图,分深水区和浅水区,如果以固定的流量向蓄水池注水,下面哪个图象能大致表示水的最大深度h和时间t之间的关系( )发布:2025/6/20 12:0:2组卷:1450引用:9难度:0.7 -
 3.某市计划在偏远地区拓展“互联网+教育”新模式,为了配合新模式的运行,某企业捐赠了一批物资,已知甲,乙两辆运送物资的货车从同一地点出发,沿同一条道路行驶.它们行驶的路程s(km)与乙车行驶的时间t(h)之间的图象如图所示,观察图象并回答下列问题:
3.某市计划在偏远地区拓展“互联网+教育”新模式,为了配合新模式的运行,某企业捐赠了一批物资,已知甲,乙两辆运送物资的货车从同一地点出发,沿同一条道路行驶.它们行驶的路程s(km)与乙车行驶的时间t(h)之间的图象如图所示,观察图象并回答下列问题:
(1)货车 先出发;(填“甲”或“乙”)
(2)货车乙行驶一段路程后出现了故障,停下来修车,货车乙停留修车的时间为 h;
(3)货车乙修好后行驶的速度与故障前行驶的速度一样吗?为什么?
(4)若货车甲始终匀速行驶,请问货车甲出发后多久与货车乙相遇?发布:2025/6/20 12:0:2组卷:74引用:1难度:0.6


